칼만필터 대충 어떻게 동작하는건진 알고 있긴했는데
오랜만이라 한번 정리하고 파이썬 구현으로 넘어감

칼만 필터는 주어진 상태 데이터와 시스템 모델을 가지고
이전에 구현한 필터와 같이 노이즈 필터링과 관측치로 올바른 상태를 추정하는 필터를 의미함
여기서 상태 데이터란 이전에 구현한 전압, 소나 거리를 사용할수 있기도하지만
로보틱스에서 사용되는 ekf slam에서는 로봇과 랜드마크의 (x, y) 좌표를 확장 칼만 필터로 추정해냄
위 그림에서 시스템 행렬 A, 오차 공분산 행렬 P, 시스템 노이즈를 의미하는 Q, 출력행렬 H, 측정 노이즈 R 가 있는데
보통 칼만 필터에서 다루는 상태 값은 전압, 초음파 거리 같이 하나가 아닌
slam의 예시에선 x_robot, y_robot, theta_robot, x_landmark1, y_landmark2, ....여러 개라 행렬의 형태, 상태 공간으로 표현하게됨
A : 시스템 행렬
Q : 시스템 노이즈
P : 오차 공분산 행렬
H : 측정값 출력 행렬
R : 측정 노이즈
K : 칼만 이득

시스템 행렬 A는 상태 x가 다음 시점에서 어떻게 변하는지 나타내는 행렬이다.
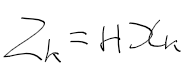
측정 값 z_k = H x_k로
H는 측정 행렬을 나타내며 x_k와 곱했을때 측정값이 튀어나오도록 하는 행렬임

칼만 이득 K_k는 측정값으로 얼마나 예측값을 보정할지 다루는 계수로
측정 노이즈 R가 크다 -> 칼만 이득은 작아짐 -> 측정 노이즈가 크다면 측정 값을 덜 반영함
오차 공분산 예측 P_bar k가 크다 -> 칼만 이득은 커짐 -> 측정 값을 더 반영한다
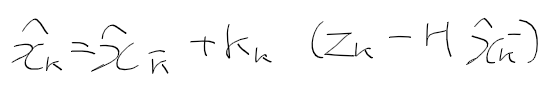
칼만 필터를 이용한 추정값 hat x_k는
hat x_k = hat x_bar k + K_k ( z_k - H hat x_bar k)로 구해진다.
칼만 이득 K_k에 따라 측정 값을 얼마나 반영시킬지 조절함
(z_k - H hat x_bar k)는 실제 측정값 - 예측 측정갑의 오차를 의미한다.

오차 공분산 행렬 예측값은 앞뒤로 시스템행렬 A를 곱해줘서 구한다.
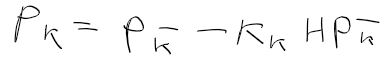
오차 공분산 행렬은 예측 오차 공분산 행렬 - 칼만 이득 * 관측 행렬 * 예측 오차 공분산 행렬인데 P_bar k로 묶으면 아래와 같다.
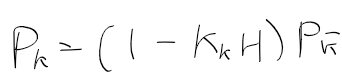
오차 공분산은 추정 결과가 얼마나 올바른지 나타냄
결과가 올바르면 오차 공분산 행렬은 작아짐
말이 많이 지저분해졌는데 대충 정리하면
칼만 필터는 필터링, 상태 추정하는 필터
관측 값과 예측 관측 값의 차이(실 상태 값과 예측 상태 추정치 차이) 에 따라 칼만 게인을 조절해서
관측 값을 얼마나 반영시킬지 조정함
쓰고 보니까 원서에서는
prediction, correction이라 해서
이전엔 예측과 갱신이라고 표현했던거같은데
이미 이렇게 쓴거 그냥 나둠
대충 로직 설명은 여기까지가고 구현 들어감
데이터는 지난번에 만든 전압 데이터 사용ㅇ

import numpy as np
def get_volt():
w = 0 + 4 * np.random.normal()
z = 14.4 + w
return z
for _ in range(10):
print(get_volt())
지금 사용하는 상태는 전압 v 하나뿐이라
A H Q R P에서 행렬이라고 할게 없음
측정 노이즈 R 같은 경우에는
갯 볼티지 함수에서 4 * 정규분포(0, 1)을 해가지구
R을 4로 줌
x는 볼티지 기저 값을 14.4로 해서 14로 주고
A, H는 변환 할게 없이 그대로 쓰므로 1
시스템 노이즈 Q는 뭐라할게 없어서 0
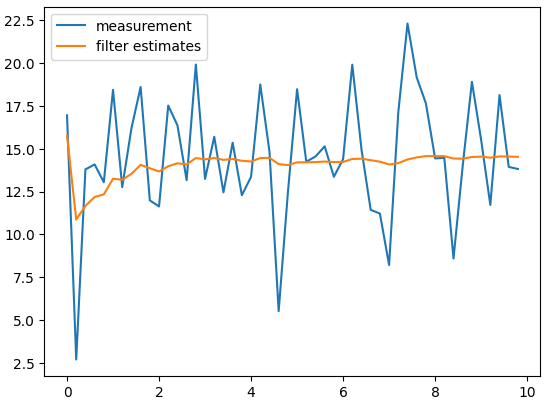
추정하는 상태값이 볼트 1개 뿐이라 뭔가 하는것같은 느낌은 안들지만
동작은 잘되긴 한다.
import matplotlib.pyplot as plt
A = 1
H = 1
Q = 0
R = 4
x = 14
P = 6
def kf(x, P, z):
x_pred = A * x
P_pred = A * P * A + Q
K = P_pred * H / (H * P_pred * H + R)
x_est = x_pred + K * (z - H * x_pred)
P_est = P_pred - K * H * P_pred
return x_est, P_est
t_list = np.arange(0, 10, 0.2)
volt_list = []
kf_list = []
x_est = 0
for _ in range(len(t_list)):
volt = get_volt()
if x_est == 0:
x_est = x
P_est = P
x_est, P_est = kf(x_est, P_est, volt)
volt_list.append(volt)
kf_list.append(x_est)
plt.plot(t_list, volt_list, label="measurement")
plt.plot(t_list, kf_list, label="filter estimates")
plt.legend()'컴퓨터과학 > 필터' 카테고리의 다른 글
| 칼만필터 파이썬 - 6. 칼만 필터를 이용한 추적기 구현 (0) | 2023.10.03 |
|---|---|
| 칼만필터 파이썬 - 5. 칼만 필터를 이용한 위치로 속도 계산 (0) | 2023.10.02 |
| 칼만필터 파이썬 - 3. 저주파 통과 필터 (0) | 2023.10.02 |
| 칼만필터 파이썬 - 2. 평균 이동 필터 (0) | 2023.10.02 |
| 칼만필터 파이썬 - 1. 평균 필터 (0) | 2023.10.02 |