깜지로 쓰려는 블로그

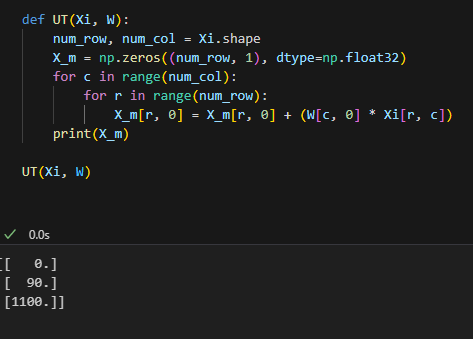
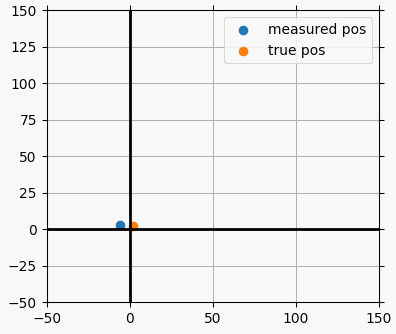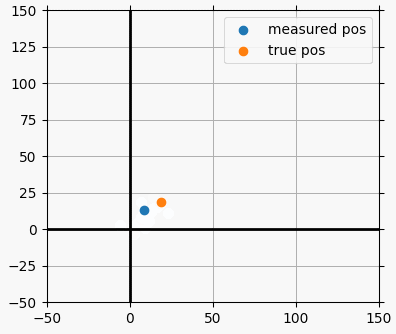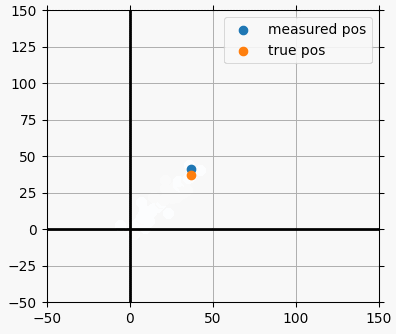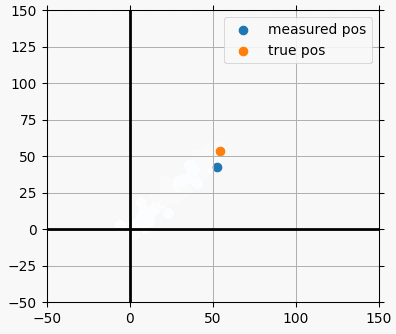
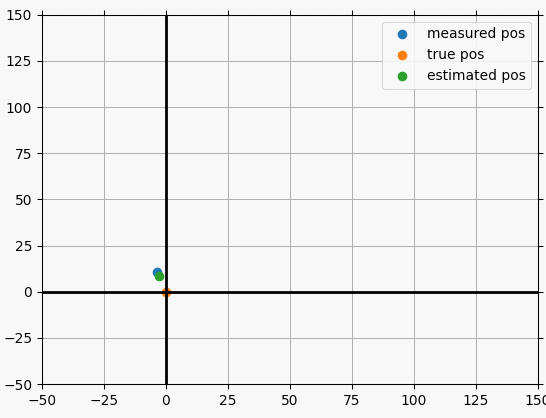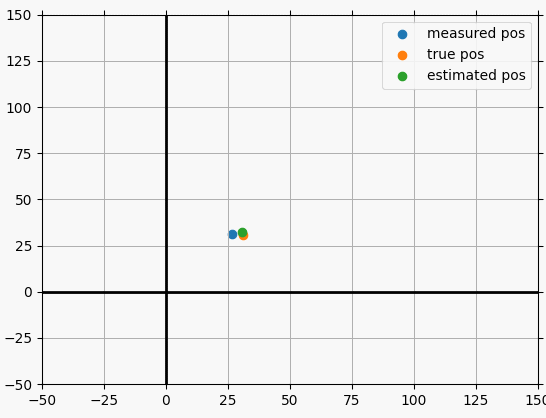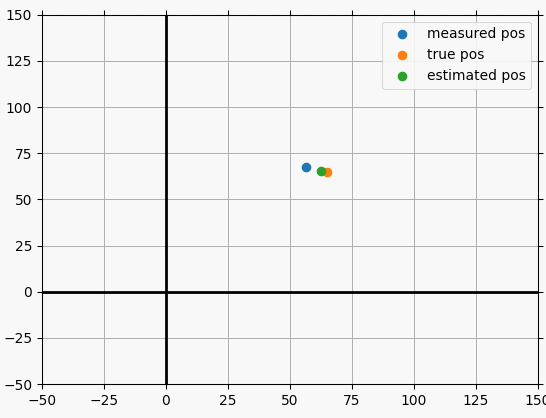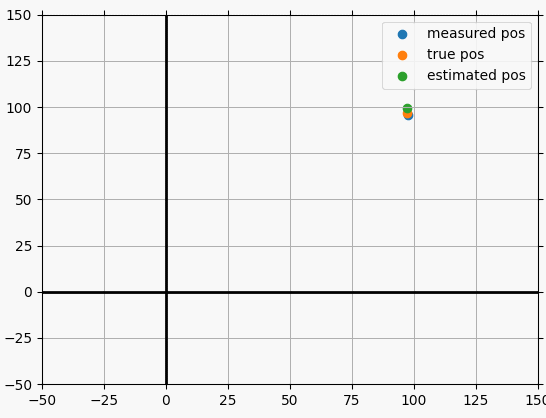
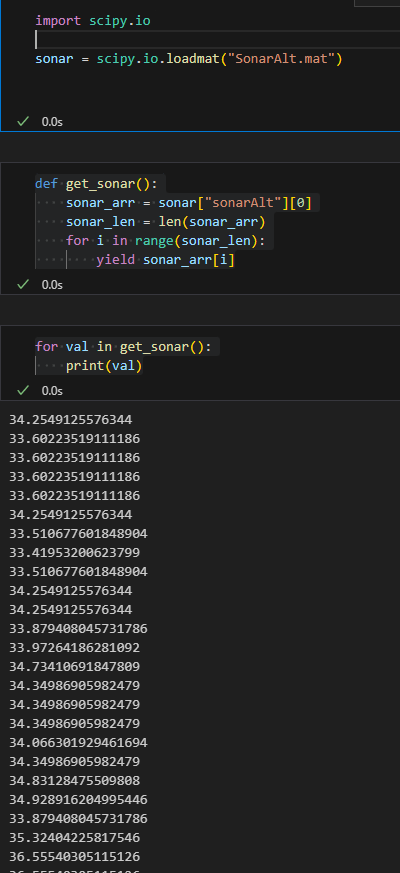
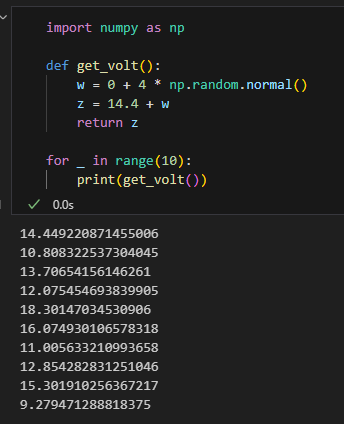
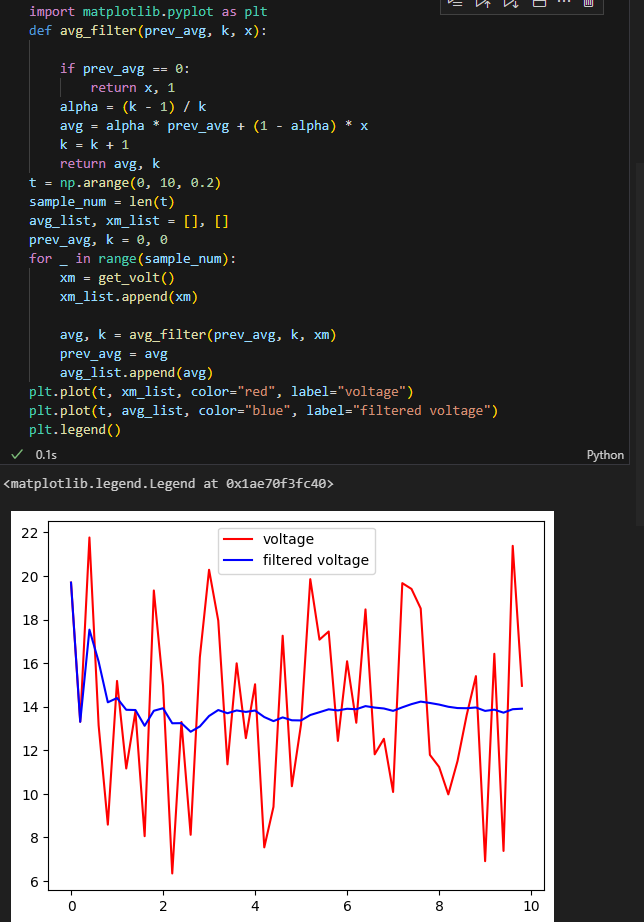
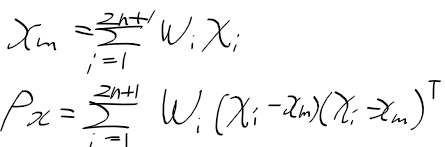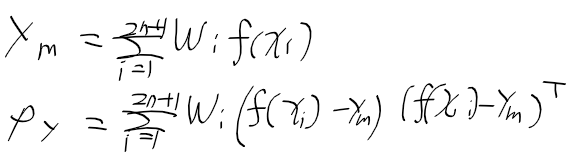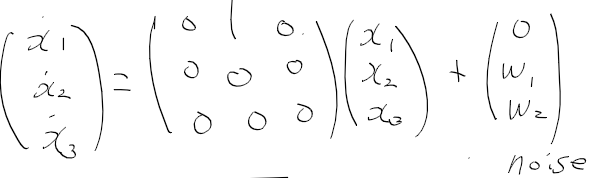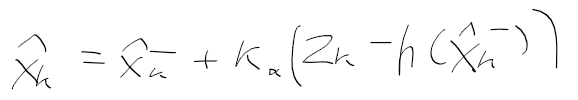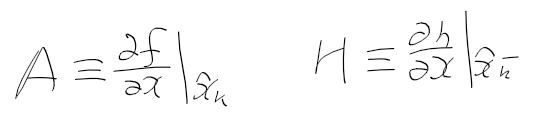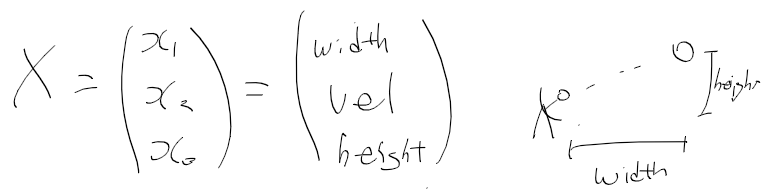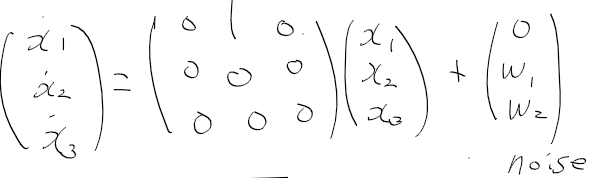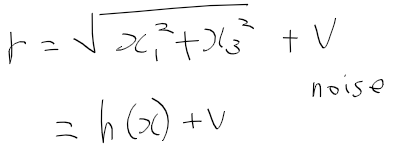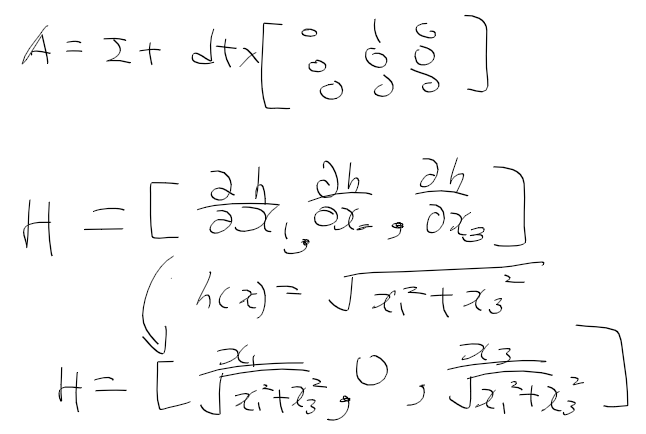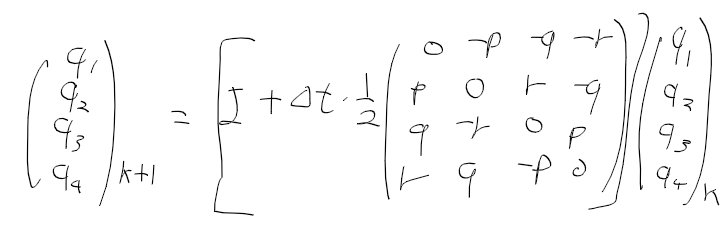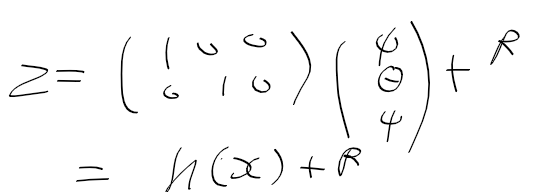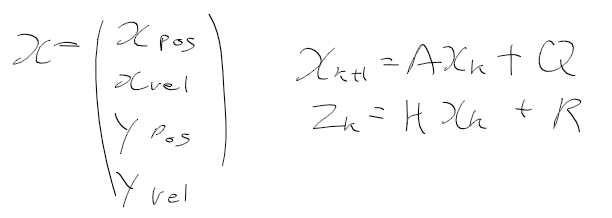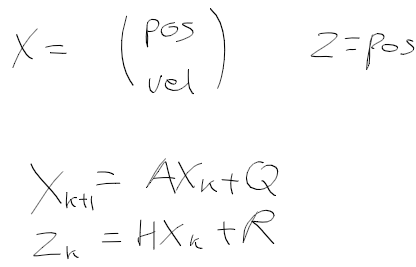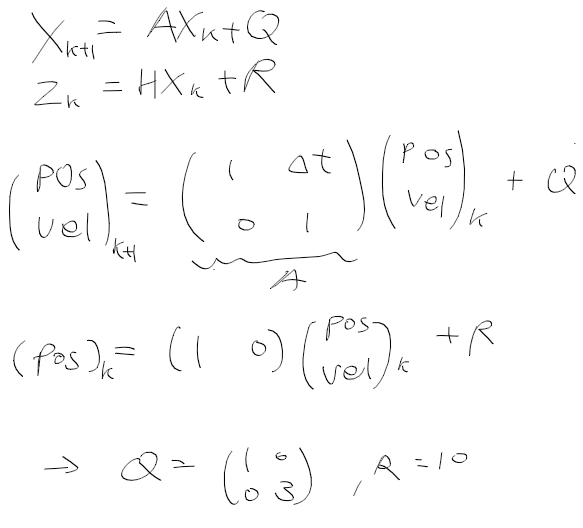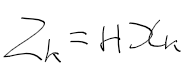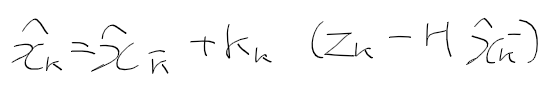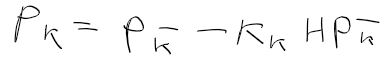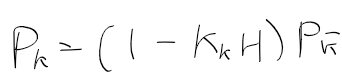칼만필터 파이썬 하는것도 이제 거의 다 되간다.

파티클 필터도 전에 공부했던거라 대충 이해하고 있다.

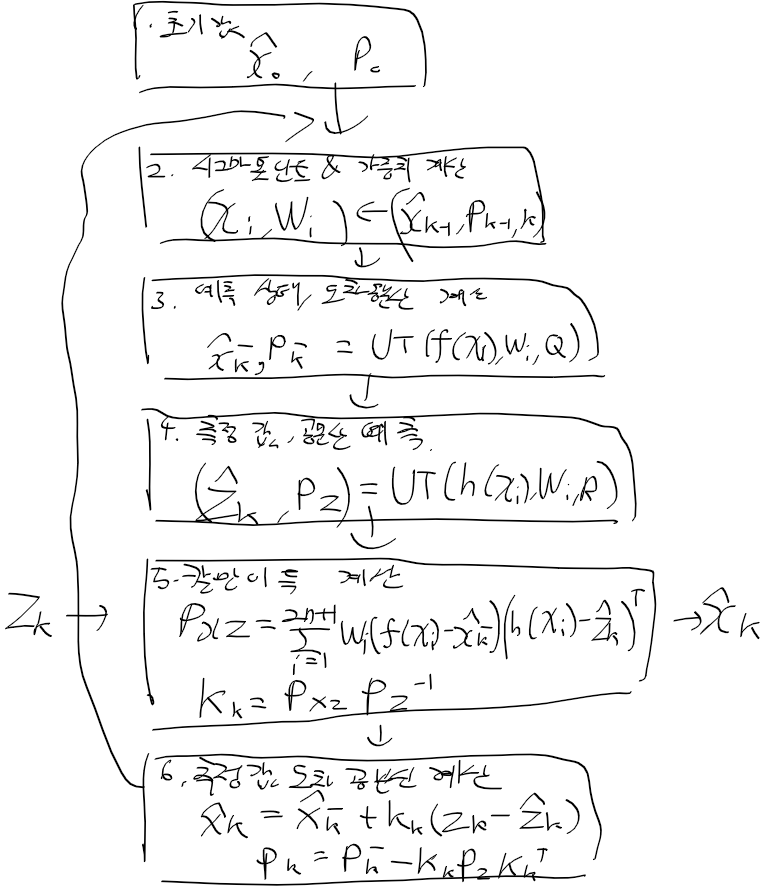
무향 칼만필터와 차이라면

무향 칼만필터에서는 시그마포인트라고 하는 점 몇개를 기준으로 관측치랑 다뤘다면

파티클필터는 많은 양의 파티클들을 생성해서 관측치를 보고

가중치를 조절해서 리샘플링을 반복하는 방식이었던걸로 기억하는데

컨셉 이해뒤 매트랩 코드 돌려본것 말곤 안했던거같은데

이번엔 파이썬으로 구현

파티클 필터 로직부터 보자

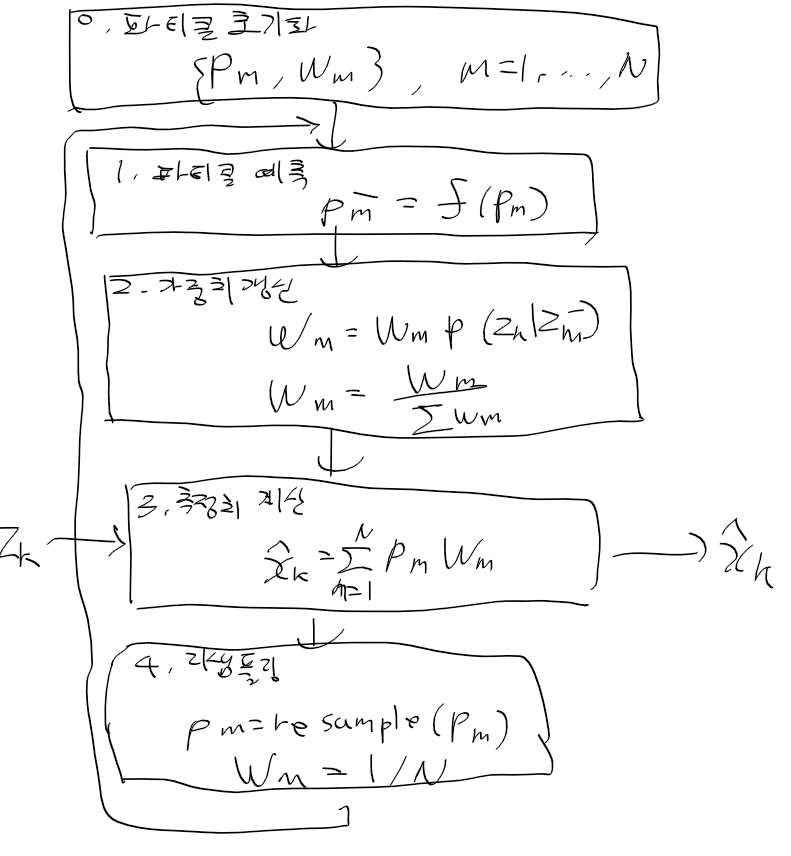
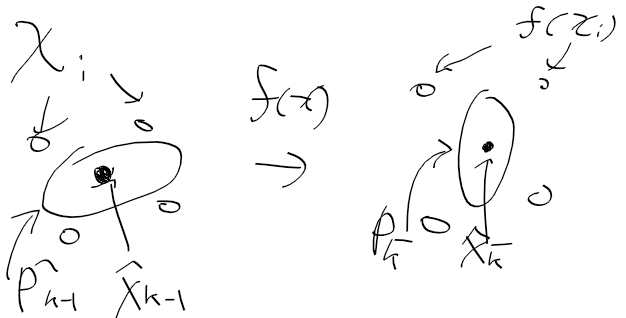
맨 처음에는 파티클들을 보통 균일 분포로 전체 영역에 뿌리고,

가중치는 1 / N(파티클 전체 수) 만큼 할당한다

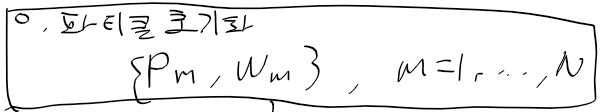
그리고 fx로 전체 파티클들에 대해  적용해서 파티클의 다음 상태를 예측한다

현재 관측치와 각 파티클의 예상 관측치를 비교해서

각 파티클들의 가중치를 조정한다.

실제 관측치와 파티클에서 예상 관측치 오차가 작을수록 더 큰 가중을 받는다.

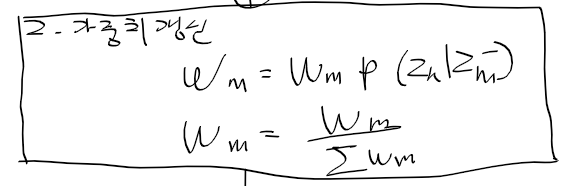
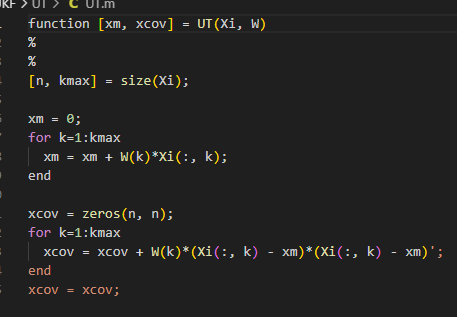
전체 파티클들의 가중 평균을 구하여

현재 상태 추정치를 구해낸다.

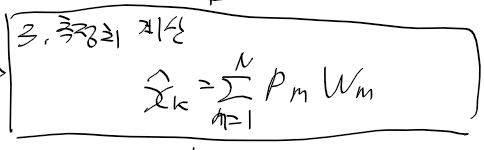
파티클들을 리샘플링을 수행한뒤 다음 타임 스탭으로 넘어간다

보통 리샘플링 알고리즘에선 가중치가 높은 쪽에 가까운 파티클들을 재생성해내는 식으로 감.

여기선 SIR 순차적 중요도 리샘플링을 쓴다고하는데

파이썬 코드로 어캐 할수있을랑가 싶네

파티클 필터를 이용한 라이더 물체 추적

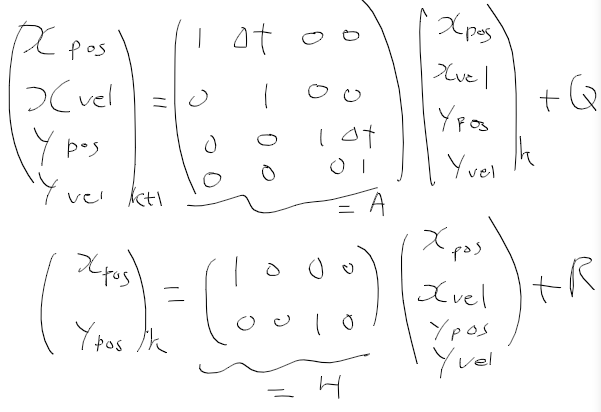
상태 변수, 시스템 모델, 측정 모델을 정리하면 다음과 같다

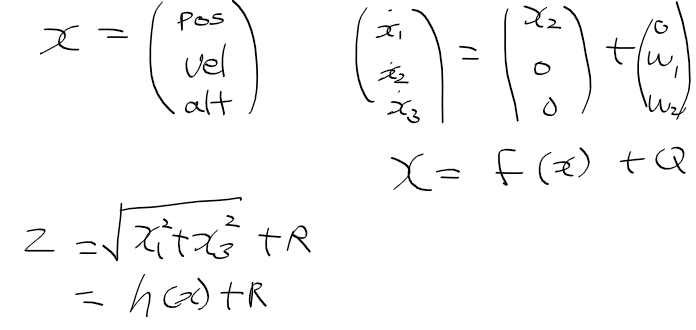
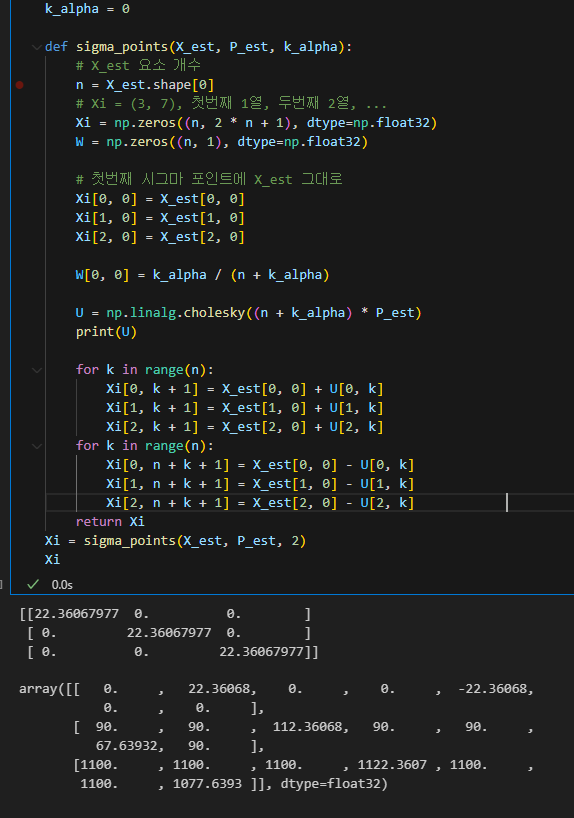
일단 파티클 필터를 구현하기 앞서 초기 파티클과 가중치 부터 초기화하자

전에 로보틱스에서 파티클필터를 다룰땐 균일분포로 했던거같은데

지금은 다른 문제라 그런가 정규 분포로 사용함

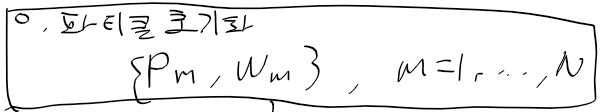
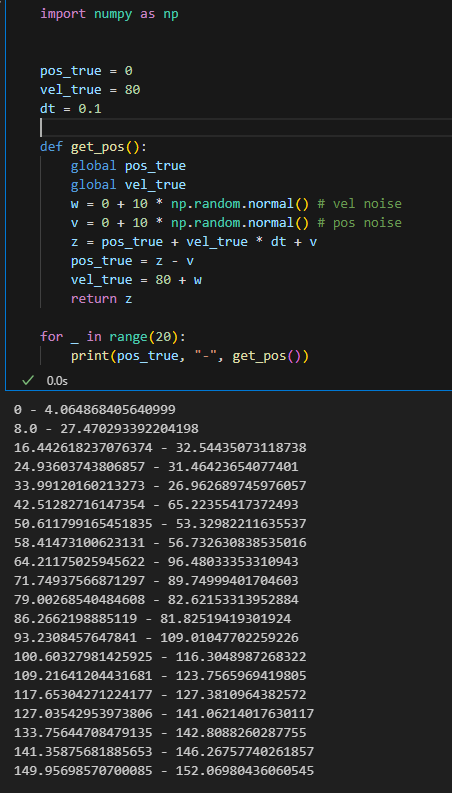
대충 초기 값들이 잘 구해짐

import numpy as np

X_est = np.array([[0, 90, 1100]]).T
N_particle = 1000

particles = np.random.normal(0, 1, (3, N_particle))
particles[0, :] = X_est[0][0] + 0.1 * X_est[0][0] * particles[0, :]
particles[1, :] = X_est[1][0] + 0.1 * X_est[1][0] * particles[1, :]
particles[2, :] = X_est[2][0] + 0.1 * X_est[2][0] * particles[2, :]
W = np.ones((1, N_particle)) * 1 / N_particle

시스템 함수를 이산 시스템으로 만들고, 관측 함수도 구현

def fx(X_est, dt):
    A = np.array([
        [0, 1, 0],
        [0, 0, 0],
        [0, 0, 0]
    ])
    A = np.eye(3) + dt * A
    X_pred = A @ X_est
    return X_pred

def hx(X_pred):
    x1 = X_pred[0][0]
    x3 = X_pred[2][0]
    Z_pred = np.sqrt(x1**2 + x3**2)
    return Z_pred

이번엔 가중치 갱신 구현할 차례인데

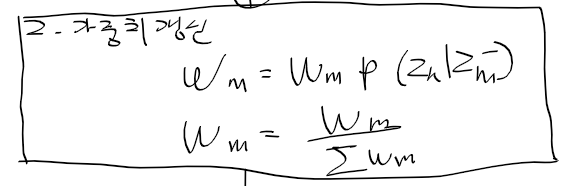
여기 적혀있는 normpdf가 정규밀도 함수라

여기다 x 값을 넣으면 정규밀도 함수값이나오는거같다

아래 매트랩 예시보면 mu = 2, sigma = 1일때 x = 2인 위치의 확률이 가장 높은 0.4정도가 나온다.

즉 실제 z와 다양한 k 중 pt로부터 얻은 hx = z가 가장 가까울 수록 높은 값을 갖는다.

적다보니 말이 이상한데 가장 실제에 가까운 파티클의 가중치를 높이는 혁활

일단 z 자리가 x 값

mu 자리는 파티클 기준 관측 예측치

분산은 10

그러면 파이썬에선 이를 대체할 함수가 뭐가 있나..

for k = 1:Npt
  wt(k) = wt(k)*normpdf(z, hx(pt(:,k)), 10);
end
wt = wt / sum(wt);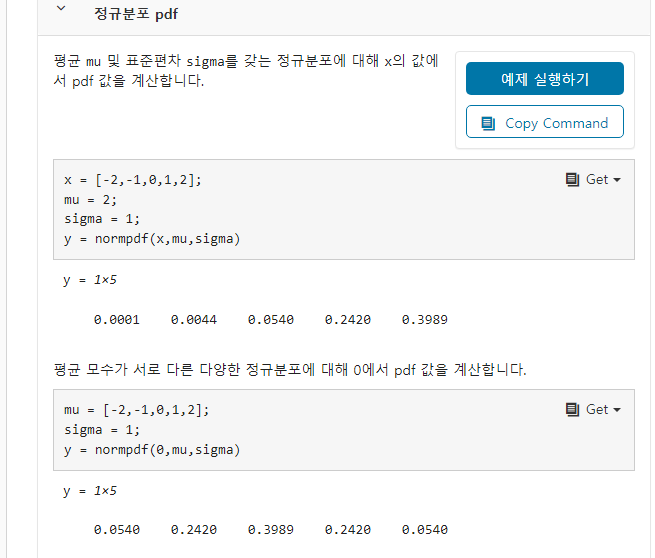

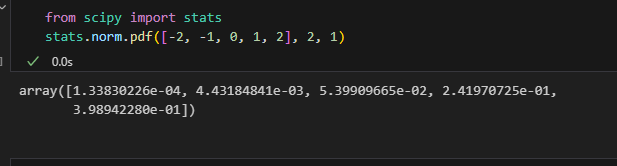
대충 찾아보니 사이파이에 있는 걸 쓰면 될듯하다.

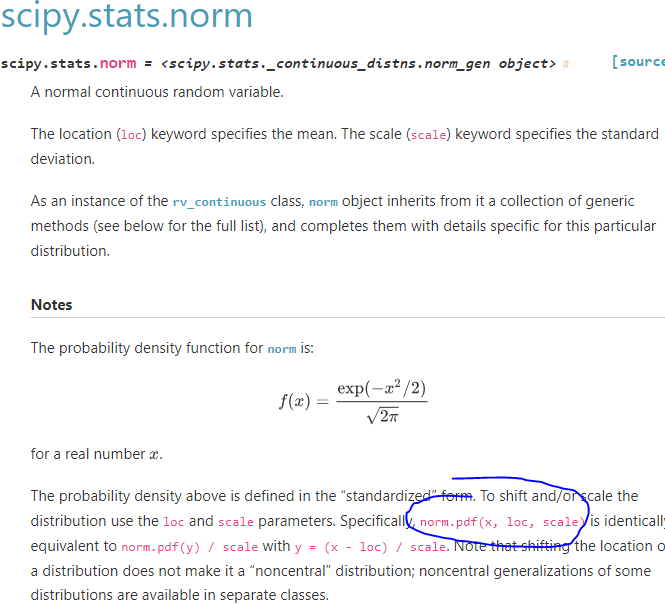
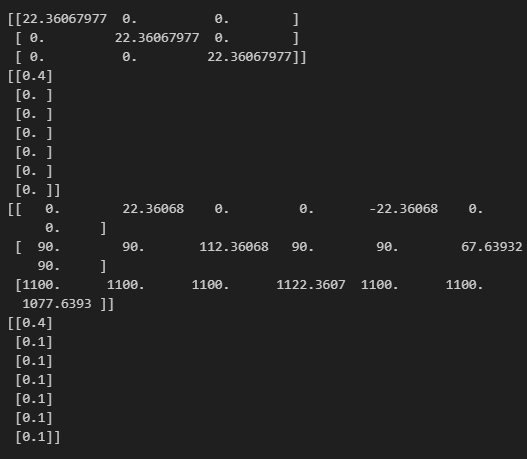
위에서 본 매트랩 예제랑 동일하게 만들어봤는데 

값이 비슷한거 봐서 맞는것같네

이제 추정 상태 구현 차례

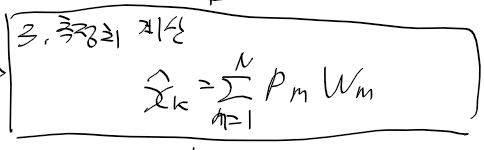
파티클은 3x 1000

가중치는 1 x 1000

가중합을 구하려면 P 행렬곱 W.T 하면

X에 알맞게 3 x 1 행렬이 나온다.

이제 거의다 구현하긴 했는데

가장 어려운 리샘플링 로직이 남았다.

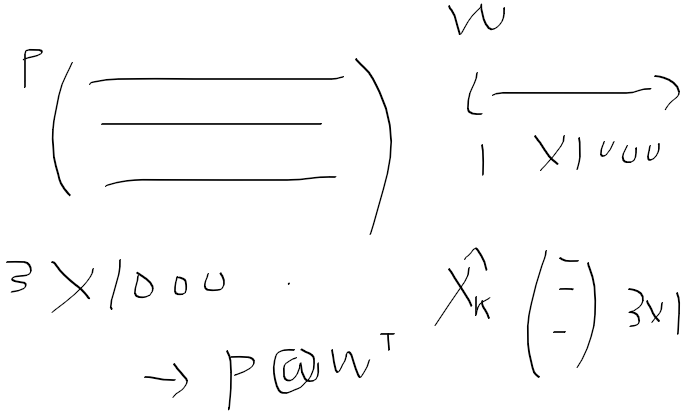
def pf(z, dt):
    global particles, W
    for k in range(N_particle):
        particles[:, k] = fx(particles[:, k], dt) + np.random.normal(0, 1, (3))
    
    for k in range(N_particle):
        W[0, k] = W[0, k] * stats.norm.pdf(z, hx(particles[:, k].reshape(-1, 1)), 10)
    W = W / sum(W[0,:])
    X_est = particles @ W.T

SIR 로직 이거 처음봤을때 뭔소린가 이해하기 정말 어려웠는데

지금은 대충은 이해된다.

가중치는 지금 1 x 1000 형태 행렬인데

정규화를 해서 전체를 합하면 1이된다.

이를 누적확률 분포 구간별로 구분하면 이런식이 된다.

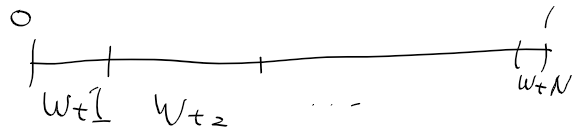
이 구간 전체에다가 균일 분포를 따르는 점들을 놓자

그러면 좁은 구간에는 점들이 적을 것이고

넓은 구간에는 점들이 많다.

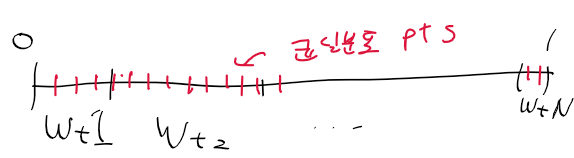
점이 많은 구간은 중요한 파티클

점이 작은 구간은 안중요한 파티클로 보고

중요도가 높은 파티클들 중심으로 리샘플링을 수행한다.

로직은 대충 알지만 이걸 어케 파이썬으로 구현하냐

일단 매트랩 함수를 찾아가면서 비슷한거 찾아쓰거나 만들어야지.

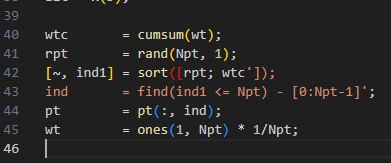
일단 cumsum은 누적 확률 분포 같은걸 만드는데

shape는 그대로 유지된다.

근대 보통 이런거 넘파이에 대부분 구현되어있다.

W 누적 분포 구하기위해 일단 임시로 관측치, 직선거리 z = 1101로 놓고 한번 가중치 누적 분포 출력하면 이런식

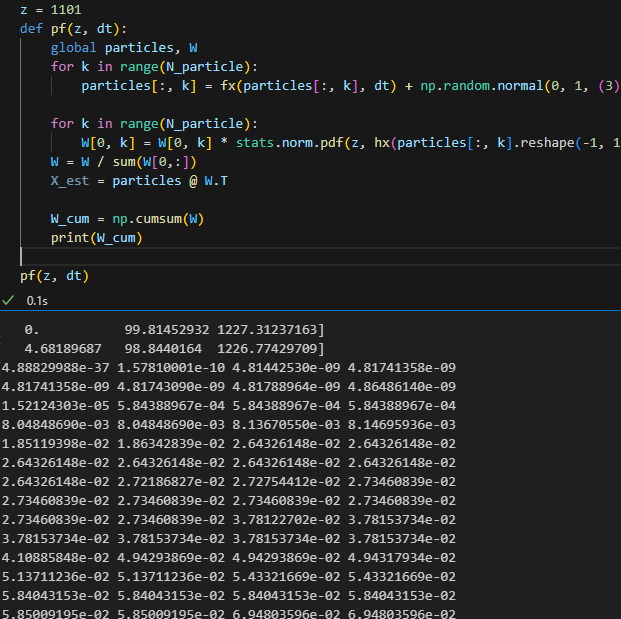
균일 분포랑 누적분포를 만들긴 했는데 매트랩 코드 그대로 구현하기가 좀 어려운데

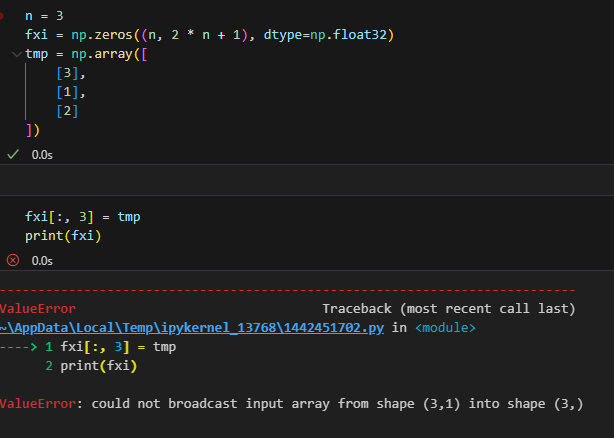
아 파이썬 데이터 타입떄문에 되게 골치아프다.

파티클이 1000개다 보니까 소숫점 매우 낮은데까지 가는데

저 로직은 이해 안되고 

그냥 위에서 중요 가중치 인덱스 찾는 로직을 억지로 루프 돌려서 만들긴 했다.

인덱스별로 균일 분포 포인트가 몇개 있는지를 구했는데

다음 문제는 파티클을 어떻게 새로 생성하는가다

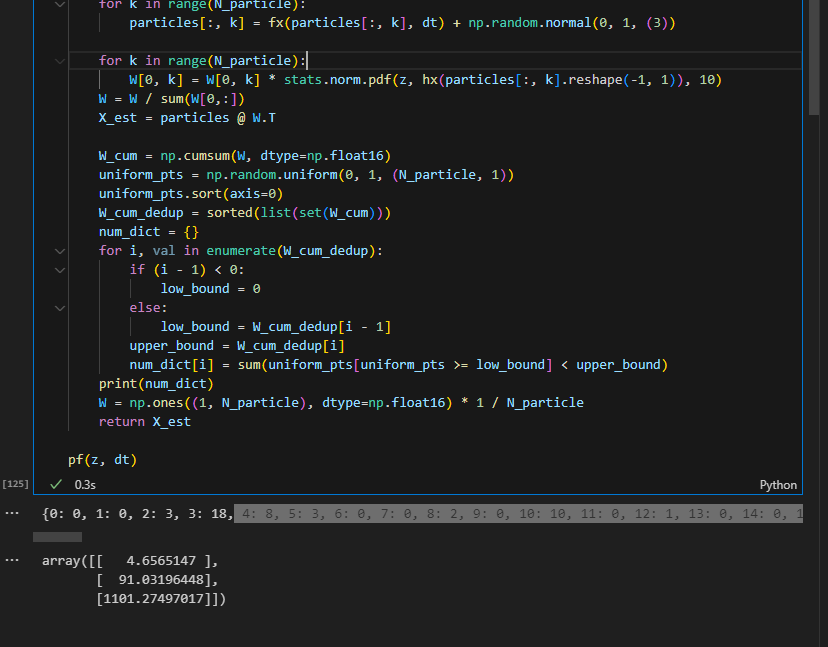
0이 아닌 인덱스들을 모아서

그 인덱스에 해당하는 파티클을 + 정규분포해서 균일분포 속한 갯수만큼 생성시키자

10번 파티클이 가장 가중치 많이 받았는데

이 가중치 구간에 균일분포 점이 100개가 들었다.

그러면 10번 파티클을 베이스로 정규분포 노이즈 추가해서 100개 만드는것으로

하는식으로 구현해야겟다.

ㅈ버ㅑㅐㅍㅂ주ㅑ잽풉재ㅑㅍㅂ주ㅑㅐㄼ우ㅐㅑ재ㅏㅂㅈ타ㅐㅔㅈ바ㅐㅔㅂ

어거지로 만들긴했는데

제대로 동작할지 모르겠다.

def pf(z, dt):
    global particles, W
    for k in range(N_particle):
        particles[:, k] = fx(particles[:, k], dt) + np.random.normal(0, 1, (3))
    
    for k in range(N_particle):
        W[0, k] = W[0, k] * stats.norm.pdf(z, hx(particles[:, k].reshape(-1, 1)), 10)
    W = W / sum(W[0,:])
    X_est = particles @ W.T
    
    W_cum = np.cumsum(W, dtype=np.float16)
    uniform_pts = np.random.uniform(0, 1, (N_particle, 1))
    uniform_pts.sort(axis=0)
    W_cum_dedup = sorted(list(set(W_cum)))
    num_dict = {}
    for i, val in enumerate(W_cum_dedup):
        if (i - 1) < 0:
            low_bound = 0
        else:
            low_bound = W_cum_dedup[i - 1]
        upper_bound = W_cum_dedup[i]
        num_dict[i] = sum(uniform_pts[uniform_pts >= low_bound] < upper_bound)

    particles_tmp = np.zeros((3, N_particle), dtype=np.float16)
    cum_idx = 0
    for key, val in num_dict.items():
        if val == 0:
            continue
        for idx in range(val):
            particles_tmp[:, cum_idx + idx] = particles[:, key] + 0.1 * particles[:, key] * np.random.normal(0, 1, (3))
        cum_idx += val
        #print(key, cum_idx, val)
    # cum idx가 1000이 안된다면(파티클 1000개 다 안채우면) 기존 파티클 재사용
    if cum_idx < 1000:
        particles_tmp[:, cum_idx:] = particles[:, cum_idx:]
    particles = particles_tmp
    W = np.ones((1, N_particle), dtype=np.float16) * 1 / N_particle
    return X_est

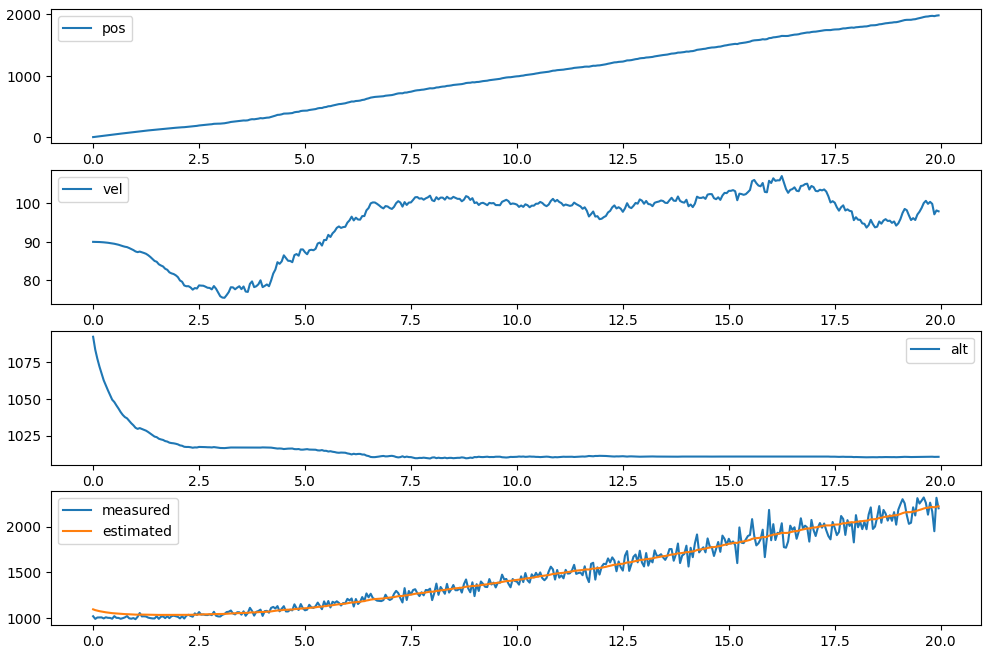
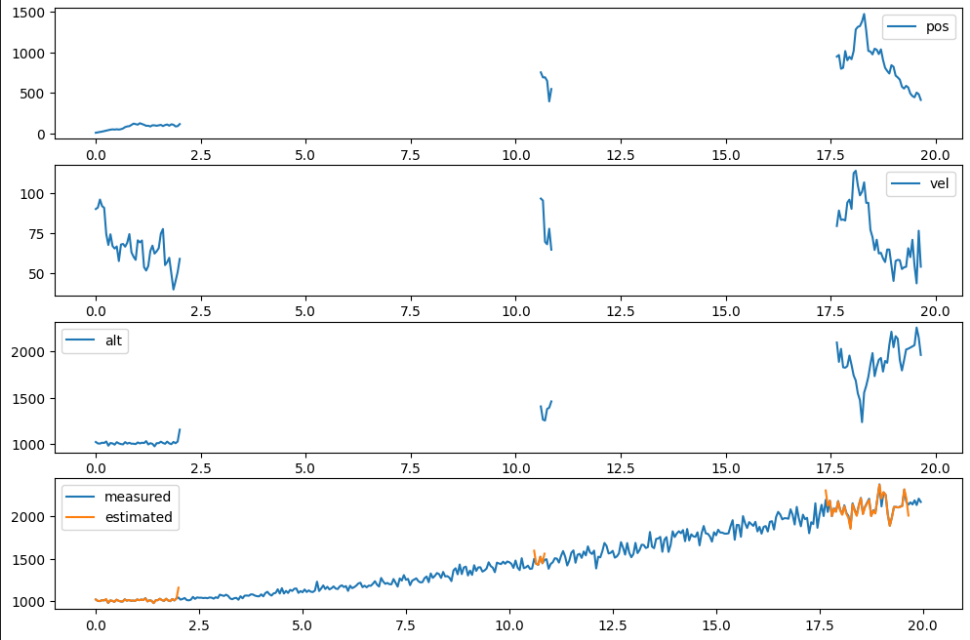
ㅠㅠ 파티클 필터 만들기는 실패

리샘플링이 문젠가 

아니면 다른 중간 로직이 문제였을까

일단 구현한 코드는 아래 첨부

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from math import sqrt


def fx(X_est, dt):
    A = np.array([
        [0, 1, 0],
        [0, 0, 0],
        [0, 0, 0]
    ])
    A = np.eye(3) + dt * A
    X_pred = A @ X_est
    return X_pred

def hx(X_pred):
    x1 = X_pred[0][0]
    x3 = X_pred[2][0]
    Z_pred = np.sqrt(x1**2 + x3**2)
    return Z_pred

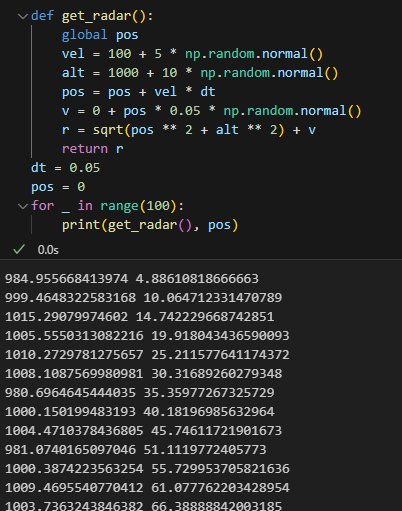
def get_radar():
    global pos
    vel = 100 + 5 * np.random.normal()
    alt = 1000 + 10 * np.random.normal()
    pos = pos + vel * dt
    v = 0 + pos * 0.05 * np.random.normal()
    r = sqrt(pos ** 2 + alt ** 2) + v
    return r

dt = 0.05
X_est = np.array([[0, 90, 1100]]).T
N_particle = 1000
pos = 0

particles = np.random.normal(0, 1, (3, N_particle))
particles[0, :] = X_est[0][0] + 0.1 * X_est[0][0] * particles[0, :]
particles[1, :] = X_est[1][0] + 0.1 * X_est[1][0] * particles[1, :]
particles[2, :] = X_est[2][0] + 0.1 * X_est[2][0] * particles[2, :]
#print(particles.shape)
W = np.ones((1, N_particle), dtype=np.float16) * 1 / N_particle

t_list = np.arange(0, 20, 0.05)
pos_list, vel_list, alt_list, z_list, dist_list = [], [], [], [], []

z = 1101
def pf(z, dt):
    global particles, W
    for k in range(N_particle):
        particles[:, k] = fx(particles[:, k], dt) + np.random.normal(0, 1, (3))
    
    for k in range(N_particle):
        W[0, k] = W[0, k] * stats.norm.pdf(z, hx(particles[:, k].reshape(-1, 1)), 10)
    W = W / sum(W[0,:])
    X_est = particles @ W.T
    
    W_cum = np.cumsum(W, dtype=np.float16)
    uniform_pts = np.random.uniform(0, 1, (N_particle, 1))
    uniform_pts.sort(axis=0)
    W_cum_dedup = sorted(list(set(W_cum)))
    num_dict = {}
    for i, val in enumerate(W_cum_dedup):
        if (i - 1) < 0:
            low_bound = 0
        else:
            low_bound = W_cum_dedup[i - 1]
        upper_bound = W_cum_dedup[i]
        num_dict[i] = sum(uniform_pts[uniform_pts >= low_bound] < upper_bound)

    particles_tmp = np.zeros((3, N_particle), dtype=np.float16)
    cum_idx = 0
    for key, val in num_dict.items():
        if val == 0:
            continue
        for idx in range(val):
            particles_tmp[:, cum_idx + idx] = particles[:, key] + 0.1 * particles[:, key] * np.random.normal(0, 1, (3))
        cum_idx += val
        #print(key, cum_idx, val)
    # cum idx가 1000이 안된다면(파티클 1000개 다 안채우면) 기존 파티클 재사용
    if cum_idx < 1000:
        particles_tmp[:, cum_idx:] = particles[:, cum_idx:]
    particles = particles_tmp
    W = np.ones((1, N_particle), dtype=np.float16) * 1 / N_particle
    return X_est


for _ in range(len(t_list)):
    z = get_radar()

    X_est = pf(z, dt)

    pos_list.append(X_est[0][0])
    vel_list.append(X_est[1][0])
    alt_list.append(X_est[2][0])
    z_list.append(z)
    dist_list.append(sqrt(X_est[0][0] ** 2 + X_est[2][0] ** 2))

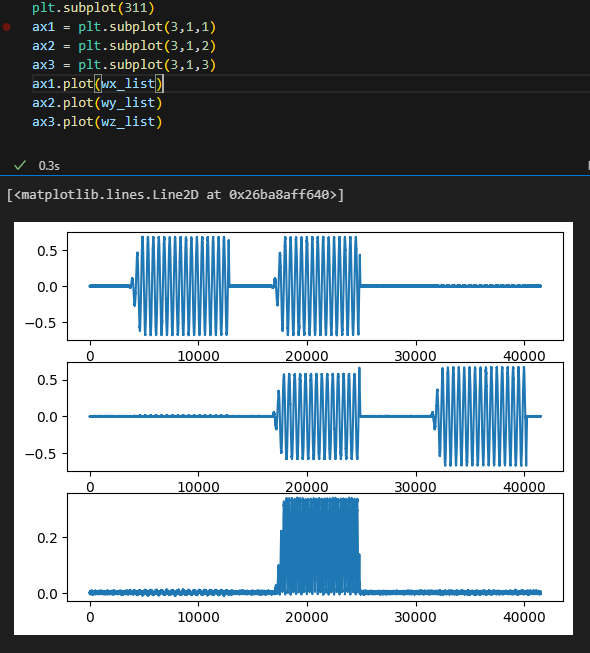
plt.subplot(411)
ax1 = plt.subplot(4,1,1)
ax2 = plt.subplot(4,1,2)
ax3 = plt.subplot(4,1,3)
ax4 = plt.subplot(4,1,4)
ax1.plot(t_list, pos_list, label="pos")
ax2.plot(t_list, vel_list, label="vel")
ax3.plot(t_list, alt_list, label="alt")
ax4.plot(t_list, z_list, label="measured")
ax4.plot(t_list, dist_list, label="estimated")
ax1.legend()
ax2.legend()
ax3.legend()
ax4.legend()
plt.gcf().set_size_inches(12, 8)

지금까지 칼만 필터 공부하면서

EKF까지만 갔지 따로 무향 칼만필터 이해하고 싶어도 이해를 못했는데 이제 무향 칼만필터 정리해보려고 함.

일단 EKF 문제가 비선형 함수를 아까 선형화 해서 자코비안만들어서 썻지만

선형화 하는 만큼 짧은 타임 스탭 동안 어느 정도 움직임을 잘 추종해내지

큰 동작이 일어나면 선형화 오차가 심해지는 문제가 있었다.

그래서 무향 칼만 필터는 선형 근사를 사용하지 않고

데이터 샘플링 하고, 무향 변환을 통해 추정 상태와 추정 오차 공분산 X_est, P_est를 구해낸다.

여기서 샘플링 되는 데이터, 대표 값을 시그마 포인트, 그리스어 표기로는 kai_i들을 선정해서 추정 상태와 오차 공분산 판단

그러면 시그마 포인트는 어캐 선정하냐는 좀 더보자

UKF 로직은 이런식

초기값 선정 다음에는 이전의 추정과 오차 공분산을 표현하는

시그마 포인트들과 각 포인트들의 가중치를 구하여야 함

\

예측 상태, 오차 공분산은 시스템 모델을 기존에 사용한 함수 f(x)가 아닌 시그마 포인트로 UT 무향 변환으로 구함

예측 측정값과, 측정 오차 공분산도 UT 변환으로 구함

칼만 이득 계산시 먼저

상태와 관측값의 공분산 P_xz 부터 계산

P_xz와 inv(P_z)의 행렬곱으로 칼만이득을 구함

이후 추정 상태와 오차 공분산은 지금까지 동일한 방식으로 계산

이거 하다보니까 파티클 필터할때 파티클 리샘플링하고 업데이트하고 했던 느낌인데

일단 무향 변환 UT는

변수 x가 x ~ N(x_m, P_x)인 정규 분포를 따름

그러면 각 시그마 포인트 kai_i와 가중치 W_i는 

여기서 u_i는 다음을 만족하는 행렬 U의 행벡터라고 하는데 이건 구현중에 좀봐야할듯

시그마 포인트의 가중 평균은 x_m

가중 공분산은 P_x 다음은 특성을 가짐

그러면 비선형 함수 y = f(x)에 시그마 포인트와 가중치를 적용해 

다음의 결과를 얻을 수  있음

다시 맨 앞에 있던 그림들 가져오자

기존의 X_est, P_est가지고 시그마 포인트 만들고

비선형 시스템 모델 f(x)를 모든 시그마 포인트에 적용해서 이동한 시그마 포인트를 얻는다

그리고 이 시그마 포인트 가중합을 통해 다음 X_est, P_est를 구한다.

이거 그냥 파티클 필터랑 거의 비슷한데

시그마 포인트를 너무 어렵게 생각해서 이해를 못했던거같다

시그마포인트 구현하기

X_est, P_est, k_alpha 값을 주면 시그마 포인트와 가중피 반환 함수 구현

아까 시그마 포인트 계산에 u_i를 구해야했는데 다음 조건을 만족하는 U의 i번째 행을 나타냈다.

여기서 말하는 U는 촐래스키분해로 구할수 있음

촐래스키 분해를 하면 하삼각행렬과 삼상각행렬로 나누어짐

시그마 포인트 구현하다가 중간에 잠깐 찍은거

여기서 X_est 요소는 3개 므로

Xi 첫번째는 X_est 그대로

Xi 둘, 셋, 내 번째 까지는 X_est + U 

Xi 다섯, 여섯, 일곱까지는 X_est - U하내

여기서 가중치 W도 추가해서 반환해주면 구현완료인데

가중치 구현하다보니 뭔가 이상한게

W = zeros(n, 1)을 줬었다.

X_est 요소는 3개라, 시그마포인트는 7개가 되는대

W은 3,1이 아닌 7, 1이여야 한다

일단 잘못된거면 나중에 고치고 이렇게 수정

k_alpha를 2로주고, 시그마 포인트가 7개여서 그런가

첫번째 시그마 포인트 X_est의 가중치는 0.4고 나머지 6개는 0.1로 되었다.

import numpy as np

X_est = np.array([[0, 90, 1100]]).T
P_est = 100 * np.eye(3)
k_alpha = 0

def sigma_points(X_est, P_est, k_alpha):
    # X_est 요소 개수
    n = X_est.shape[0]
    # Xi = (3, 7), 첫번째 1열, 두번째 2열, ...
    Xi = np.zeros((n, 2 * n + 1), dtype=np.float32)
    W = np.zeros((2*n+1, 1), dtype=np.float32)
    
    # 첫번째 시그마 포인트에 X_est 그대로
    Xi[0, 0] = X_est[0, 0]
    Xi[1, 0] = X_est[1, 0]
    Xi[2, 0] = X_est[2, 0]
    
    W[0, 0] = k_alpha / (n + k_alpha)
    
    U = np.linalg.cholesky((n + k_alpha) * P_est)
    print(U)
    print(W)
    for k in range(n):
        Xi[0, k + 1] = X_est[0, 0] + U[0, k]
        Xi[1, k + 1] = X_est[1, 0] + U[1, k]
        Xi[2, k + 1] = X_est[2, 0] + U[2, k]
        W[k + 1, 0] = 1 / (2 * (n + k_alpha))
    for k in range(n):
        Xi[0, n + k + 1] = X_est[0, 0] - U[0, k]
        Xi[1, n + k + 1] = X_est[1, 0] - U[1, k]
        Xi[2, n + k + 1] = X_est[2, 0] - U[2, k]
        W[n + k + 1, 0] = 1 / (2 * (n + k_alpha))
    return Xi, W
Xi, W = sigma_points(X_est, P_est, 2)
print(Xi)
print(W)

무향 변환 구현하기

이번에는 시그마 포인트들의 평균과 공분산을 계산해내면 된다

size는 아마 행렬 크기 반환함수일텐데

n, kmax 반환한다는건 무슨 말일까

kmax 가 열 자리니까 시그마 포인트 개수 받는다는 소린거같은데

지금 Xi가 3, 7이니 그냥 넘파이 쉐이프로 뽑아내면 될듯

가중평균 구현은 이거 참고하면될듯

아 ... 참 곤란한게 매트랩은 행렬 알아서 맞추니 그냥 변수 그대로 준거같은데

파이썬에선 이런식으로 똑같이 구현할수가 없다

가중 평균 계산하는 로직 자체는 간단한데 잠깐 좀 해맴

원래 이렇게 루프 두번 할게 아니라 넘파이 선형 연산하면 되는데 머리가 안따라간다.

일단 이렇게 진행함

가중 공분산도 계산하긴 했는데 이게 맞는건진 잘 모르겠다

결과가 맞는지나 봐야지 ㅜ

일단 무향 변환도 구현 끝

def UT(Xi, W):
    num_row, num_col = Xi.shape
    X_m = np.zeros((num_row, 1), dtype=np.float32)
    for c in range(num_col):
        for r in range(num_row):
            X_m[r, 0] = X_m[r, 0] + (W[c, 0] * Xi[r, c])
            X_cov = np.zeros((num_row, num_row), dtype=np.float32)

    for c in range(num_col):
        X_cov = X_cov + W[c, 0] * (Xi[:, c].reshape(-1, 1) - X_m) @ (Xi[:, c].reshape(-1, 1) - X_m).T
    
    return X_m, X_cov
UT(Xi, W)

UKF로 라이다 물체 추적하기

지금까지 시그마포인트랑 무향 변환도 구현했다.

UKF 구현 과중에서 필요한게 시그마 포인트를 함수 f(x)에 대입, 가중화를 해서 

동작후 예측상태,예측 오차 공분산 Y_m, P_y를 구해야한다.

일단 여기서 사용하는 f(x)는 이전에 라이더 추적 구현할때 쓴대로 다음을 이산 시스템으로 구현하면 된다.

대충 함수 fx는 이런식인데

우리가 쓸껀 그냥 상태 x를 넣고 끝내느게아니라

시그마 포인트들을 사용하므로 시그마 포인트 전체에 대한 가중 평균, 공분산 구현으로 만들어줘야한다ㅣ..

def fx(X_est, dt):
    A = np.array([
        [0, 1, 0],
        [0, 0, 0],
        [0, 0, 0]
    ])
    A = np.eye(3) + dt * A
    X_pred = A @ X_est
    return X_pred

시그마 포인트들의 fx, 이들을 모은 3 x 7 형태의 fxi 변수를 만들려고하는데

이런식으로 넣으려고 해도 브로드캐스트 에러때매 안된다.

다른 방식이야 있겠지만, 지저분하게라도 구현해야할듯

1. 기존 X_est, P_set로부터 시그마 포인트 취득

2. 시그마 포인트들을 함수 f(x)에 대입해서 fxi를 구한다.

3. 시그마 포인트들의 무향변환으로 X_pred와 P_pred를 얻어낸다.

이제 무향 칼만필터의 중간까지는 왔다.

관측을 추가하고 테스트 돌리면 끝

def UKF(X_est, P_est, z, dt):
    Xi, W = sigma_points(X_est, P_est)
    fxi = np.zeros((n, 2 * n + 1), dtype=np.float32)
    for k in range(0, 2 * n + 1):
        fx_xi = fx(Xi[:, k].reshape(-1, 1), dt)
        fxi[0, k] = fx_xi[0, 0]
        fxi[1, k] = fx_xi[1, 0]
        fxi[2, k] = fx_xi[2, 0]
    X_pred, P_pred = UT(fxi, W, Q)

여기서 관측도 무향변환을 하긴 할건데

라이더 예제에선 관측할게 직선 거리 1개 뿐이였다.

n 대신 m = 1로 놓고 hxi 도 구해보자 hxi shape는 m x 2n + 1 = 1 x 7이되겟다

(관측치 1) x (시그마 포인트 7개)

여기서 사용하는 함수 hx는 직선 거리 반환하는 함수

fxi[:, k]하면 (3,) 1차원이 들어가버려서 리쉐이프로 2차원으로 만들어 넣어줌

def hx(X_pred):
    x1 = X_pred[0][0] # width
    x3 = X_pred[2][0] # height
    z_pred = sqrt(x1 ** 2 + x3 **2)
    return z_pred

def UKF(X_est, P_est, z, dt):
    Xi, W = sigma_points(X_est, P_est)
    fxi = np.zeros((n, 2 * n + 1), dtype=np.float32)
    for k in range(0, 2 * n + 1):
        fx_xi = fx(Xi[:, k].reshape(-1, 1), dt)
        fxi[0, k] = fx_xi[0, 0]
        fxi[1, k] = fx_xi[1, 0]
        fxi[2, k] = fx_xi[2, 0]
    X_pred, P_pred = UT(fxi, W, Q)

    hxi = np.zeros((m, 2 * n + 1))
    for k in range(2 * n + 1):
        hxi[0, k] = hx(fxi[:, k].reshape(-1, 1))

이제 UKF도 다끝나간다 상태 x, 관측 z에 대한 오차공분산

P_xz만 구현하면

칼만 이득이 나오고, 최종 추정치도 계산 가능

아ㅡ자읒빏즈앚부페뱌ㅜ대릅댜ㅐ으쟁ㅈㅂㄹㅈ브ㅔㄹㅈ브벶

ㅇ나므ㅐ푸냡훕재ㅐ이,ㅈㅂ[ㅐㅐㅇ재ㅔ주랴ㅐㅈ부랴ㅐ,ㅂ

행렬 형태 떄문에 이게 맞나 좀 해매고 다녔는데

잘못 만든것 같으면서도 동작은 잘 된다

칼만 게인 shape이  3 x 1이고, P_z가 z가 한개뿐이라 1 x 1이다

P_est 계산할때 K @ P_z @ K.T 행렬 계산이

(3 x 1) @ ( 1 x 1) @ (1 x 3) 이런식인데 내가 생각했던 행렬곱과는 좀 아니여서 맞는건지 아닌지 긴가민가 했느데

일단 동작은 잘되는것 같아보이니까 그냥 여기서 마무리

데이터 취득과 UKF,  차트 플로팅까지 아래 코드에 다 모아둠

import numpy as np
import matplotlib.pyplot as plt
from math import sqrt


def get_radar():
    global pos
    vel = 100 + 5 * np.random.normal()
    alt = 1000 + 10 * np.random.normal()
    pos = pos + vel * dt
    v = 0 + pos * 0.05 * np.random.normal()
    r = sqrt(pos ** 2 + alt ** 2) + v
    return r

def hx(X_pred):
    x1 = X_pred[0][0] # width
    x3 = X_pred[2][0] # height
    z_pred = sqrt(x1 ** 2 + x3 **2)
    return z_pred

def fx(X_est, dt):
    A = np.array([
        [0, 1, 0],
        [0, 0, 0],
        [0, 0, 0]
    ])
    A = np.eye(3) + dt * A
    X_pred = A @ X_est
    return X_pred


def UT(Xi, W, Q):
    num_row, num_col = Xi.shape
    X_m = np.zeros((num_row, 1), dtype=np.float32)
    for c in range(num_col):
        for r in range(num_row):
            X_m[r, 0] = X_m[r, 0] + (W[c, 0] * Xi[r, c])
            X_cov = np.zeros((num_row, num_row), dtype=np.float32)

    for c in range(num_col):
        X_cov = X_cov + W[c, 0] * (Xi[:, c].reshape(-1, 1) - X_m) @ (Xi[:, c].reshape(-1, 1) - X_m).T
    X_cov = X_cov + Q
    return X_m, X_cov

def sigma_points(X_est, P_est, k_alpha=0):
    # X_est 요소 개수
    n = X_est.shape[0]
    # Xi = (3, 7), 첫번째 1열, 두번째 2열, ...
    Xi = np.zeros((n, 2 * n + 1), dtype=np.float32)
    W = np.zeros((2*n+1, 1), dtype=np.float32)
    
    # 첫번째 시그마 포인트에 X_est 그대로
    Xi[0, 0] = X_est[0, 0]
    Xi[1, 0] = X_est[1, 0]
    Xi[2, 0] = X_est[2, 0]
    
    W[0, 0] = k_alpha / (n + k_alpha)
    
    U = np.linalg.cholesky((n + k_alpha) * P_est)
    for k in range(n):
        Xi[0, k + 1] = X_est[0, 0] + U[0, k]
        Xi[1, k + 1] = X_est[1, 0] + U[1, k]
        Xi[2, k + 1] = X_est[2, 0] + U[2, k]
        W[k + 1, 0] = 1 / (2 * (n + k_alpha))
    for k in range(n):
        Xi[0, n + k + 1] = X_est[0, 0] - U[0, k]
        Xi[1, n + k + 1] = X_est[1, 0] - U[1, k]
        Xi[2, n + k + 1] = X_est[2, 0] - U[2, k]
        W[n + k + 1, 0] = 1 / (2 * (n + k_alpha))
    return Xi, W

n = 3
m = 1
dt = 0.05
pos = 0
t_list = np.arange(0, 20, 0.05)
pos_list, vel_list, alt_list, z_list, dist_list = [], [], [], [], []


def UKF(X_est, P_est, z, dt):
    Xi, W = sigma_points(X_est, P_est)
    fxi = np.zeros((n, 2 * n + 1), dtype=np.float32)
    for k in range(0, 2 * n + 1):
        fx_xi = fx(Xi[:, k].reshape(-1, 1), dt)
        fxi[0, k] = fx_xi[0, 0]
        fxi[1, k] = fx_xi[1, 0]
        fxi[2, k] = fx_xi[2, 0]
    X_pred, P_pred = UT(fxi, W, Q)

    hxi = np.zeros((m, 2 * n + 1))
    for k in range(2 * n + 1):
        hxi[0, k] = hx(fxi[:, k].reshape(-1, 1))
    z_pred, P_z = UT(hxi, W, R)

    P_xz = np.zeros((n, m), dtype=np.float32)
    for k in range(2 * n + 1):
        x_error = fxi[:, k].reshape(-1, 1) - X_pred
        z_error = hxi[:, k].reshape(-1, 1) - z_pred
        P_xz = P_xz + W[k, 0] * x_error @ z_error.T
    K = P_xz @ np.linalg.inv(P_z)
    X_est = X_pred + K @ (z - z_pred)
    P_est = P_pred - K @ P_z @ K.T
    return X_est, P_est

    
Q = np.array([
    [0.01, 0, 0],
    [0, 0.01, 0],
    [0, 0, 0.01]
])
R = 100
X_est = np.array([
    [0, 90, 1100]
]).T
P_est = 10 * np.eye(3)


for _ in range(len(t_list)):
    z = get_radar()
    X_est, P_est = UKF(X_est, P_est, z, dt)

    pos_list.append(X_est[0][0])
    vel_list.append(X_est[1][0])
    alt_list.append(X_est[2][0])
    z_list.append(z)
    dist_list.append(sqrt(X_est[0][0] ** 2 + X_est[2][0] ** 2))

plt.subplot(411)
ax1 = plt.subplot(4,1,1)
ax2 = plt.subplot(4,1,2)
ax3 = plt.subplot(4,1,3)
ax4 = plt.subplot(4,1,4)
ax1.plot(t_list, pos_list, label="pos")
ax2.plot(t_list, vel_list, label="vel")
ax3.plot(t_list, alt_list, label="alt")
ax4.plot(t_list, z_list, label="measured")
ax4.plot(t_list, dist_list, label="estimated")
ax1.legend()
ax2.legend()
ax3.legend()
ax4.legend()
plt.gcf().set_size_inches(12, 8)

아ㅏㅏㅏㅏㅏㅏ 농띠 치고싶은데

너무 놀았다

지금까지 사용한 칼만필터는 

시스템 모델이 선형 모델인 경우에만 사용 가능하였다.

하지만 실제 현실 현상은 비선형 모델인 경우가 많은데 

이를 칼만 필터로 모델링하기 위해

1차 태일러 전개로 비선형 모델을 선형화해서 사용하게 되었음

뭐가 비선형 시스템인지 아닌지는

이전에 파이썬 로보틱스인가 다른데서 메트랩 코드 보고 이해했었는지 가물가물한데

EKF 로봇 위치 추정 따라 구현하면서 꽤 이해됬었지만

설명하라면 잘 못하겠다.

일단 기존에 칼만 필터는 행렬을 사용했지만 비선형 시스템 모델을 다루기 위해선 비선형 함수를 사용함

비선형 함수로 바뀌면서 X 추정치도 이런식으로 바뀐다

그러면 기존의 A, H 자리에 들어가는건 비선형 함수 f, h를 x로 편미분 시켜준게 들어간다.

뭔 소린가 싶겠지만 코드 보는게 나을듯

1. EKF를 이용한 레이더 추적

조건 : 물체는 고도, 속도 일정함

상태 : 수평 거리, 속도, 고도

모르는거 : 속도, 고도

* 수평 거리와 고도를 자주 쓰는 단어인 width, height로 대충 적음

horizontal distance나 vertical distance 쓰자니 안맞는것 같기도하고 너무 길어

고도, 속도가 일정하다는 조건을 따르면 

A행렬은 이런식이되고, 속도가 일정 = 노이즈가 없다(?)라 치면 시스템 모델은 이런식으로 정리된다.

측정 모델같은 경우

레이더서 물체까지 직선 거리, 유클리디안 거리를 얻는데 이 거리는

sqrt(width **2 + height **2)로부터 얻을수 있으므로 노이즈 포함하면 이런식이됨

대충 관측치를 갖고 width, vel, height 다 계산해내갯다는거같은데

그러면 수평 거리만 알고 속도, 고도는 모른다는건 왜 그런걸까?

수평 거리, 속도, 고도 다 모른다해도 되지않나

일단 지금 작성한 모델들을 보면

시스템 모델은 선형 시스템이나, 관측 모델은 비선형이므로 선형화 해야함

선형화라 해봤자 우리가 자주 아는 편미분해서 편도함수 (자코비안)구하면됨

문제 ! 처음 시작할때 초기값 X가 없다.

X가 없으면 EKF(자코비안) 계산할수 없기도하고,

잘못된거 넣으면 오차가 발산하게되므로

초기 상태에 가장 잘 맞는 초기 추정치 X를 잘 설정해줘야 함

대충 ekf 구현 결과

import numpy as np
from math import sqrt

def jacobian(X_est):
    H = np.array([[0, 0, 0]])
    x1 = X_est[0][0]
    x3 = X_est[2][0]
    H[0][0] = x1 / sqrt(x1 ** 2 + x3 ** 2)
    H[0][2] = x3 / sqrt(x1 ** 2 + x3 ** 2) 
    return H

def hx(X_pred):
    x1 = X_pred[0][0] # width
    x3 = X_pred[2][0] # height
    z_pred = sqrt(x1 ** 2 + x3 **2)
    return z_pred

dt = 0.05

A = np.array([
    [0, 1, 0],
    [0, 0, 0],
    [0, 0, 0]
])
A = np.eye(3) + dt * A
Q = np.array([
    [0, 0, 0],
    [0, 0.001, 0],
    [0, 0, 0.001]
])
R = 10
X = np.array([
    [0, 90, 1100]
]).T
P = 10 * np.eye(3)

H = jacobian(X)

def ekf(z):
    X_pred = A @ X
    P_pred = A @ P @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K @ (z - hx(X_pred))
    P_est = P_pred - K @ H @ P_pred 
    return X_est, P_est

이걸 실제 동작 코드랑 합쳐줘야 한다

그전에 레이더 데이터 로드부터 구현하면..

아 고도 altitude가 있었네

그래도 그냥 매트랩 따라적음

고도는 1000으로 고정하고 노이즈 추가

속도도 100으로 고정하고 노이즈 추가

고도, 수평 거리로 직선 거리 계산하고 노이즈 추가 후 반환

def get_radar():
    global pos
    vel = 100 + 5 * np.random.normal()
    alt = 1000 + 10 * np.random.normal()
    pos = pos + vel * dt
    v = 0 + pos * 0.05 * np.random.normal()
    r = sqrt(pos ** 2 + alt ** 2) + v
    return r
dt = 0.05
pos = 0
for _ in range(100):
    print(get_radar(), pos)

레이더 데이터 가져오기도 구현했으니 

아까 구현한 EKF랑 데이터 플로팅을 합치면된다.

하고 구현하고보니

중간에 잘못 만든게 몇개 있어서 한참 찾아해맴

자코비안 계산중에 dtype을 float32안해줬더니

자동으로 int로 설정되서 그런가

자코비안 행렬 H가 자꾸 값이 0으로만 나오는것떄문에 --

아무튼 계산 결과도 잘 나온다

위치는 0 에서 계속 100씩 올라가가고

속도는 실제는 100인데, 초기치로 90을 줘서 잠깐 요동치다 대충 맞추고

고도 같은 경우 실제 1000이지만 초기치를 1100으로 줘서 처음엔 위에서 급떨어진다

직선 거리같은 경우에는 잘 필터링해서 따라간다.

import numpy as np
import matplotlib.pyplot as plt
from math import sqrt

def jacobian(X_est):
    H = np.array([[0, 0, 0]], dtype=np.float32)
    x1 = X_est[0][0]
    x3 = X_est[2][0]
    H[0][0] = x1 / sqrt(x1 ** 2 + x3 ** 2)
    H[0][2] = x3 / sqrt(x1 ** 2 + x3 ** 2)
    return H

def hx(X_pred):
    x1 = X_pred[0][0] # width
    x3 = X_pred[2][0] # height
    z_pred = sqrt(x1 ** 2 + x3 **2)
    return z_pred

def get_radar():
    global pos
    vel = 100 + 5 * np.random.normal()
    alt = 1000 + 10 * np.random.normal()
    pos = pos + vel * dt
    v = 0 + pos * 0.05 * np.random.normal()
    r = sqrt(pos ** 2 + alt ** 2) + v
    return r

def ekf(X, P, z):
    X_pred = A @ X
    P_pred = A @ P @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K * (z - hx(X_pred))
    P_est = P_pred - K @ H @ P_pred 
    return X_est, P_est

dt = 0.05
pos = 0
t_list = np.arange(0, 20, 0.05)
pos_list, vel_list, alt_list, z_list, dist_list = [], [], [], [], []

A = np.array([
    [0, 1, 0],
    [0, 0, 0],
    [0, 0, 0]
])
A = np.eye(3) + dt * A
Q = np.array([
    [0, 0, 0],
    [0, 0.001, 0],
    [0, 0, 0.001]
])
R = 10
X_est = np.array([
    [0, 90, 1100]
]).T
P_est = 10 * np.eye(3)

for _ in range(len(t_list)):
    H = jacobian(X_est)
    z = get_radar()
    X_est, P_est = ekf(X_est, P_est, z)
    pos_list.append(X_est[0][0])
    vel_list.append(X_est[1][0])
    alt_list.append(X_est[2][0])
    z_list.append(z)
    dist_list.append(sqrt(X_est[0][0] ** 2 + X_est[2][0] ** 2))

plt.subplot(411)
ax1 = plt.subplot(4,1,1)
ax2 = plt.subplot(4,1,2)
ax3 = plt.subplot(4,1,3)
ax4 = plt.subplot(4,1,4)
ax1.plot(t_list, pos_list, label="pos")
ax2.plot(t_list, vel_list, label="vel")
ax3.plot(t_list, alt_list, label="alt")
ax4.plot(t_list, z_list, label="measured")
ax4.plot(t_list, dist_list, label="estimated")
ax1.legend()
ax2.legend()
ax3.legend()
ax4.legend()

2. 오일러각 EKF 적용하기

지난 글에 작성한 자이로, 가속도계 데이터에 칼만필터를 사용했는데

이번에는 오일러각을 EKF로 구해보려고한다.

칼만 필터로 오일러각 계산할때는 각속도 p,q,r로 행렬 A를 놓고 phi, theta, psi를 계산할수 없어서

쿼터니언으로 변환해서 사용했었다.

그때 사용한 행렬 A는 다음 같은 식인데

EKF로 비선형 함수를 선형화해서 쓰면 p, q, r로도 phi, theta, psi를 계산할수 있다

일단 p, q, r과 파이 세타 프사이 관계는 이런식

하지만 EKF에선 비선형 함수를 선형화해서 자코비안 행렬로 시스템 모델 A를 구할수 있음

관측 모델의 경우 가속도계로 파이, 세타만 구하였으므로

H는 다음 형태가 된다.

이제 대충 내용 정리됬으니 기존 자이로, 가속도 센서 퓨전 코드를 EKF로 고쳐보면

기본 로직은 이런식으로

dt = 0.01
t_list = np.linspace(0, 415, 41500)
phi_list, theta_list, psi_list = [], [], []

X_est = np.array([[0, 0, 0]]).T
P_est = 10 * np.eye(3)

H = np.array([
    [1, 0, 0],
    [0, 1, 0]
])
Q = np.array([
    [0.0001, 0, 0],
    [0, 0.0001, 0],
    [0, 0, 0.1]
])
R = 10 * np.eye(2)

for (p, q, r), (ax, ay, az) in zip(get_gyro(), get_accel()):

    rates = (p, q, r)
    phi, theta = accel_euler(ax, ay, az)
    z = np.array([[phi, theta]]).T
    X_est, P_est = ekf_euler(z, rates, X_est, P_est, dt)

    phi_list.append(X_est[0][0] * 180 / pi)
    theta_list.append(X_est[1][0] * 180 / pi)
    psi_list.append(X_est[2][0] * 180 / pi)
    

plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(t_list, phi_list)
ax2.plot(t_list, theta_list)
ax3.plot(t_list, psi_list)

오일러각 ekf에서

이전 X_est와 가져온 p, q, r  rates로 비선형 함수 fx와 자코비안 A 계산

이후 X_est와 P_est 계산해서 반환하면 파이와 세타는 지난글 오일러각 구한것과 비슷하게 나오는데

프사이는 좀 다르다 뭘 틀리게 한건질 모르겟네

def fx(X_est, rates, dt):
    phi = X_est[0][0]
    theta = X_est[1][0]

    p = rates[0]
    q = rates[1]
    r = rates[2]

    X_pred = np.array([[0, 0, 0]], dtype=np.float32).T
    X_pred[0][0] = p + q * sin(phi) * tan(theta) + r * cos(phi) * tan(theta)
    X_pred[1][0] = q * cos(phi) - r * sin(phi)
    X_pred[2][0] = q * sin(phi) / cos(theta) + r * cos(phi) / cos(theta)
    # math에는 sec가 없어서 sec는 cos의 역수이므로 곱 sec 대신 / cos로 계산

    X_pred = X_est + X_pred * dt 
    return X_pred


def jacob_A(X_est, rates, dt):
    phi = X_est[0][0]
    theta = X_est[1][0]

    p = rates[0]
    q = rates[1]
    r = rates[2]

    A = np.zeros((3, 3), dtype=np.float32)
    A[0, 0] = q * cos(phi) * tan(theta) - r * sin(phi) * tan(theta)
    A[0, 1] = q * sin(phi) / (cos(theta)**2) + r * cos(phi) / (cos(theta)**2)
    A[0, 2] = 0

    A[1, 0] = -q * sin(phi) - r * cos(phi)
    A[1, 1] = 0
    A[1, 2] = 0

    A[2, 0] = q * cos(phi) / cos(theta) - r * sin(phi) / cos(theta)
    A[2, 1] = q * sin(phi) / cos(theta) * tan(theta) + r * cos(phi) / cos(theta) * tan(theta)
    A[2, 2] = 0

    A = np.eye(3) + A * dt
    return A
    

def accel_euler(ax, ay, az):
    g = 9.8
    theta = asin( ax / g)
    phi = asin(-ay / (g * cos(theta)))
    return phi, theta


def ekf_euler(z, rates, X_est, P_est, dt):
    A = jacob_A(X_est, rates, dt)
    X_pred = fx(X_est, rates, dt)
    P_pred = A @ P_est @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K @ (z - H @ X_pred)
    P_est = P_pred - K @ H @ P_pred
    return X_est, P_est

자이로, 가속도계 EKF를 이용한 센서 퓨전 전체 코드

from math import atan2, sin, cos, asin, tan
from math import pi
import scipy.io
import matplotlib.pyplot as plt
import numpy as np

gyro = scipy.io.loadmat("EulerEKF/ArsGyro.mat")
def get_gyro():
    wx = gyro["wx"]
    wy = gyro["wy"]
    wz = gyro["wz"]

    gyro_len = len(wx)
    for i in range(gyro_len):
        yield wx[i][0], wy[i][0], wz[i][0]

accel = scipy.io.loadmat("EulerEKF/ArsAccel.mat")
def get_accel():
    ax = accel["fx"]
    ay = accel["fy"]
    az = accel["fz"]

    accel_len = len(ax)
    for i in range(accel_len):
        yield ax[i][0], ay[i][0], az[i][0]


def fx(X_est, rates, dt):
    phi = X_est[0][0]
    theta = X_est[1][0]

    p = rates[0]
    q = rates[1]
    r = rates[2]

    X_pred = np.array([[0, 0, 0]], dtype=np.float32).T
    X_pred[0][0] = p + q * sin(phi) * tan(theta) + r * cos(phi) * tan(theta)
    X_pred[1][0] = q * cos(phi) - r * sin(phi)
    X_pred[2][0] = q * sin(phi) / cos(theta) + r * cos(phi) / cos(theta)
    # math에는 sec가 없어서 sec는 cos의 역수이므로 곱 sec 대신 / cos로 계산

    X_pred = X_est + X_pred * dt 
    return X_pred


def jacob_A(X_est, rates, dt):
    phi = X_est[0][0]
    theta = X_est[1][0]

    p = rates[0]
    q = rates[1]
    r = rates[2]

    A = np.zeros((3, 3), dtype=np.float32)
    A[0, 0] = q * cos(phi) * tan(theta) - r * sin(phi) * tan(theta)
    A[0, 1] = q * sin(phi) / (cos(theta)**2) + r * cos(phi) / (cos(theta)**2)
    A[0, 2] = 0

    A[1, 0] = -q * sin(phi) - r * cos(phi)
    A[1, 1] = 0
    A[1, 2] = 0

    A[2, 0] = q * cos(phi) / cos(theta) - r * sin(phi) / cos(theta)
    A[2, 1] = q * sin(phi) / cos(theta) * tan(theta) + r * cos(phi) / cos(theta) * tan(theta)
    A[2, 2] = 0

    A = np.eye(3) + A * dt
    return A
    

def accel_euler(ax, ay, az):
    g = 9.8
    theta = asin( ax / g)
    phi = asin(-ay / (g * cos(theta)))
    return phi, theta


def ekf_euler(z, rates, X_est, P_est, dt):
    A = jacob_A(X_est, rates, dt)
    X_pred = fx(X_est, rates, dt)
    P_pred = A @ P_est @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K @ (z - H @ X_pred)
    P_est = P_pred - K @ H @ P_pred
    return X_est, P_est

dt = 0.01
t_list = np.linspace(0, 415, 41500)
phi_list, theta_list, psi_list = [], [], []

X_est = np.array([[0, 0, 0]]).T
P_est = 10 * np.eye(3)

H = np.array([
    [1, 0, 0],
    [0, 1, 0]
])
Q = np.array([
    [0.0001, 0, 0],
    [0, 0.0001, 0],
    [0, 0, 0.1]
])
R = 10 * np.eye(2)

for (p, q, r), (ax, ay, az) in zip(get_gyro(), get_accel()):

    rates = (p, q, r)
    phi, theta = accel_euler(ax, ay, az)
    z = np.array([[phi, theta]]).T
    X_est, P_est = ekf_euler(z, rates, X_est, P_est, dt)

    phi_list.append(X_est[0][0] * 180 / pi)
    theta_list.append(X_est[1][0] * 180 / pi)
    psi_list.append(X_est[2][0] * 180 / pi)
    

plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(t_list, phi_list)
ax2.plot(t_list, theta_list)
ax3.plot(t_list, psi_list)

센서 퓨전 진짜 오랜만에 보는데 

일단 먼저 자이로 각속도로 오일러 각 구하기 구현 시작

1. 자이로로 부터 얻은 각속도로 오일러 각 구하기

일단 자이로 각속도 데이터부터 읽어오기 구현

제너레이터로 루프마다 가져오게 만듬

각속도 wx, wy, wz

import scipy.io

gyro = scipy.io.loadmat("ArsGyro.mat")
def get_gyro():
    wx = gyro["wx"]
    wy = gyro["wy"]
    wz = gyro["wz"]

    gyro_len = len(wx)
    for i in range(gyro_len):
        yield wx[i], wy[i], wz[i]

for wx, wy, wz in get_gyro():
    print(wx, wy, wz)


get_gyro()

xyz니까 한번 플로팅해주려고 하는데 할때마다 서브플롯 어캐햇는지 잊어먹는다

import matplotlib.pyplot as plt

plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax2 = plt.subplot(3,1,3)

대충 이거랑 get gyro랑 섞으면 이래 나온다.

wx_list = []
wy_list = []
wz_list = []

for wx, wy, wz in get_gyro():
    wx_list.append(wx)
    wy_list.append(wy)
    wz_list.append(wz)

plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(wx_list)
ax2.plot(wy_list)
ax3.plot(wz_list)

2. 각속도 -> 오일러각 변환하기

이번에는 각속도 wx,wy,wz를 pqr이라 하자

이걸 오일러각 phi theta psi 로 바꾸도록 구현

얻어내고자 하는 오일러각(변화량)은

기존의 오일러 각으로 아래 3 x 3 행렬 구하고 p q r 과 곱하면 나옴

매트랩 코드를 파이썬으로 구현하는데

이전 파이 세타 프사이를 매개변수로 넣어버릴까 싶다가

그냥 메트랩 코드 따라서 전역으로 나둠

일단 대충 구현하면 이런식이다

from math import cos, sin, tan

prev_phi = 0
prev_theta = 0
prev_psi = 0 
def gyro_euler(p, q, r, dt):
    sin_phi = sin(prev_phi)
    cos_phi = cos(prev_phi)
    cos_theta = cos(prev_theta)
    tan_theta = tan(prev_theta)

    phi = prev_phi + dt * (p + q * sin_phi * tan_theta + r * cos_phi * tan_theta)
    theta = prev_theta + dt * (q * cos_phi - r * sin_phi)
    psi = prev_psi + dt * (q * sin_phi / cos_theta + r * cos_phi / cos_theta)

    return phi, theta, psi

각속도 -> 오일러 변환 모듈을 플로팅함수랑 합치자

위 그래프 3개는 각속도

아래 3개는 오일러각

z축 회전은 그렇다 쳐도

x, y를 보면 오차가 누적되서 롤 피치각이 기울어진 모양을 하고있음

3. 가속도계 값 가져오기

자이로는 됫으니 가속도계 가져올 차례

자이로랑 별차이 없다 이름만 조금 고쳐줌

import scipy.io

accel = scipy.io.loadmat("ArsAccel.mat")
def get_accel():
    ax = accel["fx"]
    ay = accel["fy"]
    az = accel["fz"]

    accel_len = len(ax)
    for i in range(accel_len):
        yield ax[i], ay[i], az[i]

for ax, ay, az in get_accel():
    print(ax, ay, az)


get_accel()

이것도 플로팅해보면

잘 나온다.

ax_list = []
ay_list = []
az_list = []

for ax, ay, az in get_accel():
    ax_list.append(ax)
    ay_list.append(ay)
    az_list.append(az)

plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(ax_list)
ax2.plot(ay_list)
ax3.plot(az_list)

4. 회전하지 않고, 등속도 운동 상황 가정시 자세 구하기

이제 가속도를 쓰려고 하는데 좀 복잡하게 생김

가속도에는 회전 영향도 있고, 중력 영향도 있음

등속운동 중이고, 회전을 안한다 가정시, 위 식을 단순하게 만들어서

fx, fy, fz를 가지고 파이와 세타를 구할 수 있음

xyz 가속도로 파이 세타 가져오는 함수 구현하면 이럼

from math import asin, acos

def accel_euler(ax, ay, az):
    g = 9.8
    theta = asin( ax / g)
    phi = asin(-ay / (g * cos(theta)))
    return phi, theta

이것도 그래프 플로팅 시키면

파이, 세타

롤피치요 니까

아래 2개는 롤각과 피치각을 나타냄

import numpy as np

def accel_euler(ax, ay, az):
    g = 9.8
    theta = asin( ax / g)
    phi = asin(-ay / (g * cos(theta)))
    return phi, theta

dt = 0.01

t_list = np.linspace(0, 415, 41500)
ax_list, ay_list, az_list = [], [], []
phi_list, theta_list = [], []


for ax, ay, az in get_accel():
    phi, theta = accel_euler(ax, ay, az)
    ax_list.append(ax)
    ay_list.append(ay)
    az_list.append(az)

    phi_list.append(phi)
    theta_list.append(theta)


plt.subplot(511)
ax1 = plt.subplot(5,1,1)
ax2 = plt.subplot(5,1,2)
ax3 = plt.subplot(5,1,3)
ax1.plot(t_list, ax_list)
ax2.plot(t_list, ay_list)
ax3.plot(t_list, az_list)
ax4 = plt.subplot(5,1,4)
ax5 = plt.subplot(5,1,5)
ax4.plot(t_list, phi_list)
ax5.plot(t_list, theta_list)

5. 센서 퓨전을 통한 자세 구하기

앞서 자이로만 가지고 파이 세타 프사이 자세를

가속도계만 가지고 파이 세타 자세를 계산해봄

이번에는 kf로 자이로와 가속도 데이터 센서 퓨전함

자이로, 가속도 계 데이터 보면

자이로로 구한 자세는 오차가 누적

가속도계로 구한 자세는 오차 누적되진 않음

=> 자이로 데이터로 자세를 먼저 구하고, 누적되는 오차는 가속도 계로 보정

! 오일러각 대신 쿼터니언 사용

X를 파이 세타 프사이로 놓으면 시스템 행렬 A를 만들수가 없다

대신 쿼터니언을 사용하면 각속도 pqr과 쿼터니언을 이런식으로 정리 가능

k+1, k 이산 시간에 대해 수정하면 이런식으로 정리해서 A를 구할수 있음

쿼터니언과 오일러각 사이 관계는 이런식이라고 함

지금까지 구현한 kf에서는 

시스템 행렬 A가 고정 되어있었는데

지금 시스템 행렬 A는 각속도 pqr에 따라 계속 변해서 이전 구현 내용과는 살짝 다름

이전 kf에서는 z만 넣어줬찌만

이번 kf에는 A, z를 같이 넣는다

잠깐 구현 중에 다시 정리한다

1. 각속도 -> 시스템 행렬 A 만듬

2. 가속도계 -> 오일러각 변환 phi, theta 취득 -> 쿼터니언으로 변환하여 z로 사용

미완 코드

def kf_euler(A, z):
    X_pred = A @ X
    P_pred = A @ P @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K @ (z - H @ X_pred)
    P_est = P_pred - K @ H @ P_pred
    return X_est, P_est

dt = 0.01


X = np.array([[1, 0, 0, 0]]).T
H = np.array([
    [1, 0, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1]
])
Q = 0.0001 * np.eye(4)
R = 10 * np.eye(4)
P = np.eye(4)


for (p, q, r), (ax, ay, az) in zip(get_gyro(), get_accel()):

    A = np.array([
        [0, -p, -q, -r],
        [p, 0, r, -q],
        [q, -r, 0, p],
        [r, q, -p, 0]
    ])
    A = np.eye(4) + dt * 1/2 * A

    phi, theta = accel_euler(ax, ay, az)

내가 여기서 빠트린게 오일러각으로 쿼터니언 변환을 구현안했다

아까 그림대로 만들면 되는데 되게 복잡하네

구현하다보니 kf 결과는 쿼터니언으로 반환하니

알아보게 시각화하려면 쿼터니언을 오일러각으로 다시 바꿔줘야 한다..

이건 엄두가 안나는데 메트랩코드 그대로 파이썬으로 고쳐줌

def quaternion_to_euler(X):
    x1 = X[0][0]
    x2 = X[1][0]
    x3 = X[2][0]
    x4 = X[3][0]

    phi =  atan2( 2*(x3*x4 + x1*x2), 1 - 2*(x2**2 + x3**2) )
    theta = -asin(  2*(x2*x4 - x1*x3))
    psi =  atan2( 2*(x2*x3 + x1*x4), 1 - 2*(x3**2 + x4**2))
    return phi, theta, psi

아 하다가 겟 자이로, 가속도에서 좀 잘못구현한거같은데

wx[i] 이던걸 뒤에 [0] 인덱싱 추가해줘야 kf 계산에서 잘못안댐

import scipy.io

gyro = scipy.io.loadmat("ArsGyro.mat")
def get_gyro():
    wx = gyro["wx"]
    wy = gyro["wy"]
    wz = gyro["wz"]

    gyro_len = len(wx)
    for i in range(gyro_len):
        yield wx[i][0], wy[i][0], wz[i][0]

for wx, wy, wz in get_gyro():
    print(wx, wy, wz)


get_gyro()


import scipy.io

accel = scipy.io.loadmat("ArsAccel.mat")
def get_accel():
    ax = accel["fx"]
    ay = accel["fy"]
    az = accel["fz"]

    accel_len = len(ax)
    for i in range(accel_len):
        yield ax[i][0], ay[i][0], az[i][0]

for ax, ay, az in get_accel():
    print(ax, ay, az)

get_accel()

자이로, 가속도계를 이용해서 노이즈를 제거한채 자세 추정이 잘 되었다

아래 그림은 아까 자이로 각속도에서 오일러각 계산한 그래프인데

4, 5번째 파이 세타가 오차 누적되서 기울어졌었지만 지금은 가속도 계 덕분에 누적 오차를 제거해서 윗 그림처럼 원하는 결과 얻어내었다.

from math import atan2
from math import pi

def euler_to_quaternion(phi, theta, psi):
    sin_phi = sin(phi / 2)
    cos_phi = cos(phi / 2)
    sin_theta = sin(theta / 2)
    cos_theta = cos(theta / 2)
    sin_psi = sin(psi / 2)
    cos_psi = cos(psi / 2)

    z = np.array([
        [
            cos_phi * cos_theta * cos_psi + sin_phi * sin_theta * sin_psi,
            sin_phi * cos_theta * cos_psi - cos_phi * sin_theta * sin_psi,
            cos_phi * sin_theta * cos_psi + sin_phi * cos_theta * sin_psi,
            cos_phi * cos_theta * sin_psi - sin_phi * sin_theta * cos_psi
        ]
    ]).T
    return z

def quaternion_to_euler(X):
    x1 = X[0][0]
    x2 = X[1][0]
    x3 = X[2][0]
    x4 = X[3][0]

    phi =  atan2( 2*(x3*x4 + x1*x2), 1 - 2*(x2**2 + x3**2) )
    theta = -asin(  2*(x2*x4 - x1*x3))
    psi =  atan2( 2*(x2*x3 + x1*x4), 1 - 2*(x3**2 + x4**2))
    return phi, theta, psi

def kf_euler(A, z):
    X_pred = A @ X
    P_pred = A @ P @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K @ (z - H @ X_pred)
    P_est = P_pred - K @ H @ P_pred
    return X_est, P_est

dt = 0.01
t_list = np.linspace(0, 415, 41500)
phi_list, theta_list, psi_list = [], [], []

X = np.array([[1, 0, 0, 0]]).T
H = np.array([
    [1, 0, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1]
])
Q = 0.0001 * np.eye(4)
R = 10 * np.eye(4)
P = np.eye(4)

for (p, q, r), (ax, ay, az) in zip(get_gyro(), get_accel()):

    A = np.array([
        [0, -p, -q, -r],
        [p, 0, r, -q],
        [q, -r, 0, p],
        [r, q, -p, 0]
    ])
    A = np.eye(4) + dt * 1/2 * A
    phi, theta = accel_euler(ax, ay, az)
    z = euler_to_quaternion(phi, theta, 0)
    X, P = kf_euler(A, z)
    phi, theta, psi = quaternion_to_euler(X)

    phi_list.append(phi * 180 / pi)
    theta_list.append(theta * 180 / pi)
    psi_list.append(psi * 180 / pi)
    

plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(t_list, phi_list)
ax2.plot(t_list, theta_list)
ax3.plot(t_list, psi_list)

이번에 작성할 내용은 칼만 필터를 이용한 추적기를 만들려고 했는데

opencv 영상 처리로 얻어낸 물체 추적을 하자니 너무 복잡해질거같고

파이 게임에다가 공 그려놓고 하자니 파이 게임 경험이 없어서 하질 못하겠다

가장 간단하게 생각 나는건

plt 애니메이션 인데

어쩔수 없이 plt 애니메이션 만듬

동작은 0,0 원점에서 10,10 지점까지 직선으로 이동하는 상황을 플로팅부터 구현함

vscode ipynb matplotlib funcanimation 쓰기

아무 plt 애니메이션 예제 돌리려고하니까 동작이 안된다

찾아보니 vscode 에서 ipynb 아나콘다 파이선 인터프리터 쓰려고보니

%matplotlib notebook은 주피터 노트북이 아니면 동작안되서 그렇다는거같다

대신 이 글대로 ipympl 설치해서 플로팅 전에

%matplotlib ipympl 해주면 된다

대충 이렇게 하면 

y=x 따라 점 포인트가 0, 0 에서 10, 10으로 이동하는 애니메이션이 나온다

%matplotlib ipympl

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

fig, ax = plt.subplots()
def animate(x):
    ax.clear()
    ax.grid()
    ax.scatter(x, x)
    ax.set_xlim([0, 10])
    ax.set_ylim([0, 10])
    

ani = FuncAnimation(fig, animate, frames=np.arange(0, 10, 0.1))
plt.show()

공 위치 구현하기

일단 vscode ipynb에서 함수 애니메이션은 했는데

공 위치를 0 ~ 10은 너무 좁은거같아 0 ~ 100으로 늘림,

노이즈 고려해서 구간도 -50 ~ 150으로 늘리고 보기 좋게 축 라인도 그려줌

프레임 간격도 0.1에서 1로 변경

animate(x)로 넘어오는 x는 실제 위치니

여기다 노이즈도 첨가

이제 좀 이쁘게 보인다

%matplotlib ipympl

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

def get_ball_pos(pos_true):
    x = pos_true + 5 * np.random.normal()
    y = pos_true + 5 * np.random.normal()
    return x, y

fig, ax = plt.subplots()
def animate(pos_true):
    ax.clear()
    ax.grid()
    x, y = get_ball_pos(pos_true)
    ax.scatter(x, y, label="measured pos")
    ax.scatter(pos_true, pos_true, label="true pos")
    ax.set_xlim([-50, 150])
    ax.set_ylim([-50, 150])
    ax.axhline(linewidth=2, color='k')
    ax.axvline(linewidth=2, color='k')
    ax.legend()

ani = FuncAnimation(fig, animate, frames=np.arange(0, 100, 1))
plt.show()

시스템 행렬, 관측 행렬 등 정리하기

애니메이션, 관측값 노이즈 첨가도 했으니

kf 구현하기전에 시스템 모델을 어떻게 할지 정리하자

상태 x 는 pos x, vel x, pos y, vel y 4가지로 구성되고

관측할건 pos x, pos y가 되겠다.

그러면 시스템 행렬 A와 관측 모델 H는 다음과 같음

kf 공 추적기 구현하기

아까 실수로 get ball pos에서 z가 아닌 x, y 반환하도록 구현했다. 이거 수정하고

위에서 설명한대로 A, H 구현

나머지 Q, R, P 같은 경우는 어떻게 좋은 값 구하는 방법을 잘모르겟다 그냥 설정

전역, 지역변수 뒤죽박죽되서 코드가 좀 엉망이긴한데

대충 관측 x, y 값가지고 

실제 x, y에 가깝게 잘 추정해낸다.

출력해서 제대로 보진 않았지만 x, y vel도 잘 추정하고 있겟지

%matplotlib ipympl

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

def get_ball_pos(pos_true):
    x = pos_true + 5 * np.random.normal()
    y = pos_true + 5 * np.random.normal()
    z = np.array([[x, y]]).T
    return z

dt = 1
A = np.array([
    [1, dt, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 1, dt],
    [0, 0, 0, 1]
])
H = np.array([
    [1, 0, 0, 0],
    [0, 0, 1, 0]
])
Q = 0.01 * np.eye(4)
R = np.array([
    [10, 0],
    [0, 10]
])
P = 20 * np.eye(4)
X = np.array([
    [0, 0, 0, 0]
]).T

def kf_tracker(z):
    global P

    X_pred = A @ X
    P_pred = A @ P @ A.T + Q
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    X_est = X_pred + K @ (z - H @ X_pred)
    P = P_pred - K @ H @ P_pred
    return X_est


fig, ax = plt.subplots()

def animate(pos_true):
    global X
    print(pos_true)
    ax.clear()
    ax.grid()
    z = get_ball_pos(pos_true)

    ax.scatter(z[0][0], z[1][0], label="measured pos")
    ax.scatter(pos_true, pos_true, label="true pos")
    X_est = kf_tracker(z)
    X = X_est
    ax.scatter(X_est[0][0], X_est[2][0], label="estimated pos")
    ax.set_xlim([-50, 150])
    ax.set_ylim([-50, 150])
    ax.axhline(linewidth=2, color='k')
    ax.axvline(linewidth=2, color='k')
    ax.legend()

ani = FuncAnimation(fig, animate, frames=np.arange(0, 100, 1))
plt.show()

아깐 볼트 측정 값을 받아와서 추정하다보니

시스템 행렬이고 뭐고 할게 없었음

이번엔 위치로 속도 구하려고하는데

다루는 상태가 전압값 이 아닌

상태는 위치, 속도 두가지

이젠 행렬을 다뤄야 한다.

다루는 상태 X는 pos, vel

측정하는 값은 pos만 한다고 하자

시스템 모델 정리하면 다음과 같다,

pos는 이전 pos + 이전 속도 * dt로 구할수 있으므로

시스템 행렬 A는 다음과 같으며

관측 행렬 H의 경우 pos와 vel 중에서 pos만 뽑으면 되니 (1 0)이 된다. 

시스템 노이즈 Q와 관측 노이즈 R은 다음과 같이 설정하자

위치 값 가져오기 함수 구현

아직 사용하는 위치는 x, y같은 좌표값은 아니고 1차원 값임

초기 위치 0, 속도 80

import numpy as np


pos_true = 0
vel_true = 80
dt = 0.1

def get_pos():
    global pos_true
    global vel_true
    w = 0 + 10 * np.random.normal() # vel noise
    v = 0 + 10 * np.random.normal() # pos noise
    z = pos_true + vel_true * dt + v
    pos_true = z - v
    vel_true = 80 + w
    return z

for _ in range(20):
    print(pos_true, "-", get_pos())

위치 -> 속도, 위치 추정

일단 사용할 변수들 부터  정의하자

시스템 노이즈 Q 같은 경우 포즈 공분산 1, 속도 공분산 3놓고

X는 pos 0 vel 20으로 설정하자

오차 공분산 P는 5 * eye해서 정하고

관측 노이즈 R은 10으로 설정

import matplotlib.pyplot as plt

pos_true = 0
vel_true = 80
dt = 0.1
time_cur, time_stop = 0, 5

t_list = []
pos_true_list = []
pos_est_list = []
vel_true_list = []
vel_est_list = []

A = np.array([
    [1, dt],
    [0, 1]
])

H = np.array([
    [1, 0]
])
Q = np.array([
    [1, 0],
    [0, 3]
])
X = np.array([
    [0, 20]
]).T
P = 5 * np.eye(2)
R = 10

위치 -> 위치, 속도 계산하는 kf 로직은 거의 비슷한데

행렬 연산하다보니 연산자 @을 사용

def dv_kf(z):
    x_pred = A @ X
    P_pred = A @ P @ A.T + Q

    K_numerator = P_pred @ H.T
    K_denominator = H @ P_pred @ H.T + R
    K_denominator = np.linalg.inv(K_denominator)
    K = K_numerator @ K_denominator
    
    measurement_err = z - H @ x_pred
    x_est = x_pred + K @ measurement_err
    P_est = P_pred - K @ H @ P_pred
    return x_est, P_est

동작 로직은 다음과 같이 구현

while time_cur < time_stop:
    z = get_pos()
    X, P = dv_kf(z)

    t_list.append(time_cur)
    pos_true_list.append(pos_true)
    pos_est_list.append(X[0][0])
    vel_true_list.append(vel_true)
    vel_est_list.append(X[1][0])
    time_cur += dt

ax1 = plt.subplot(2, 1, 1)
ax2 = plt.subplot(2, 1, 2)
ax1.plot(t_list, pos_true_list, label="true pos")
ax1.plot(t_list, pos_est_list, label="kf pos")
ax1.legend()
ax2.plot(t_list, vel_true_list, label="true speed")
ax2.plot(t_list, vel_est_list, label="kf speed")
ax2.legend()

추정 결과를 보면

위치는 잘 잡긴한데

속도는 처음엔 잘 못잡다가 시간 가면서 실제 속도를 잘 추정해낸다.

속도 -> 속도, 위치 추정

먼저 데이터 가져오기 함수부터 고치자

아깐 위치 가져오기 함수였지만 

실제 거리에선 노이즈 빼고

z = vel_ true로 설정

def get_vel():
    global pos_true
    global vel_true
    w = 0 + 10 * np.random.normal() # vel noise
    vel_true = 80 + w
    pos_true = pos_true + vel_true * dt
    z = vel_true
    return z

칼만필터 로직은 변경할거 없고

X에서 위치를 뽑아내려고

H = [1, 0] 로 했던걸

속도를 뽑아낼수 있도록

H = [0, 1]로 고치가만 하면 끝

import matplotlib.pyplot as plt

def get_vel():
    global pos_true
    global vel_true
    w = 0 + 10 * np.random.normal() # vel noise
    vel_true = 80 + w
    pos_true = pos_true + vel_true * dt
    z = vel_true
    return z


pos_true = 0
vel_true = 80
dt = 0.1
time_cur, time_stop = 0, 5

t_list = []
pos_true_list = []
pos_est_list = []
vel_true_list = []
vel_est_list = []

A = np.array([
    [1, dt],
    [0, 1]
])

H = np.array([
    [0, 1]
])
Q = np.array([
    [1, 0],
    [0, 3]
])
X = np.array([
    [0, 20]
]).T
P = 5 * np.eye(2)
R = 10

def int_kf(z):
    x_pred = A @ X
    P_pred = A @ P @ A.T + Q

    K_numerator = P_pred @ H.T
    K_denominator = H @ P_pred @ H.T + R
    K_denominator = np.linalg.inv(K_denominator)
    K = K_numerator @ K_denominator

    measurement_err = z - H @ x_pred
    x_est = x_pred + K @ measurement_err
    P_est = P_pred - K @ H @ P_pred
    return x_est, P_est


while time_cur < time_stop:
    pos_true_list.append(pos_true)

    z = get_vel()
    X, P = int_kf(z)

    t_list.append(time_cur)
    pos_est_list.append(X[0][0])
    vel_true_list.append(vel_true)
    vel_est_list.append(X[1][0])
    time_cur += dt

ax1 = plt.subplot(2, 1, 1)
ax2 = plt.subplot(2, 1, 2)
ax1.plot(t_list, pos_true_list, label="true pos")
ax1.plot(t_list, pos_est_list, label="kf pos")
ax1.legend()
ax2.plot(t_list, vel_true_list, label="true speed")
ax2.plot(t_list, vel_est_list, label="kf speed")
ax2.legend()

칼만필터 대충 어떻게 동작하는건진 알고 있긴했는데

오랜만이라 한번 정리하고 파이썬 구현으로 넘어감

칼만 필터는 주어진 상태 데이터와 시스템 모델을 가지고

이전에 구현한 필터와 같이 노이즈 필터링과 관측치로 올바른 상태를 추정하는 필터를 의미함

여기서 상태 데이터란 이전에 구현한 전압, 소나 거리를 사용할수 있기도하지만

로보틱스에서 사용되는 ekf slam에서는 로봇과 랜드마크의 (x, y) 좌표를 확장 칼만 필터로 추정해냄

위 그림에서 시스템 행렬 A, 오차 공분산 행렬 P, 시스템 노이즈를 의미하는 Q, 출력행렬 H, 측정 노이즈 R 가 있는데

보통 칼만 필터에서 다루는 상태 값은 전압, 초음파 거리 같이 하나가 아닌

slam의 예시에선 x_robot, y_robot, theta_robot, x_landmark1, y_landmark2, ....여러 개라 행렬의 형태, 상태 공간으로 표현하게됨

A : 시스템 행렬

Q : 시스템 노이즈

P : 오차 공분산 행렬

H : 측정값 출력 행렬

R : 측정 노이즈

K : 칼만 이득

시스템 행렬 A는 상태 x가 다음 시점에서 어떻게 변하는지 나타내는 행렬이다.

측정 값 z_k = H x_k로

H는 측정 행렬을 나타내며 x_k와 곱했을때 측정값이 튀어나오도록 하는 행렬임

칼만 이득 K_k는 측정값으로 얼마나 예측값을 보정할지 다루는 계수로

측정 노이즈 R가 크다 -> 칼만 이득은 작아짐 -> 측정 노이즈가 크다면 측정 값을 덜 반영함

오차 공분산 예측 P_bar k가 크다 -> 칼만 이득은 커짐 -> 측정 값을 더 반영한다

칼만 필터를 이용한 추정값 hat x_k는

hat x_k = hat x_bar k + K_k ( z_k - H hat x_bar k)로 구해진다.

칼만 이득 K_k에 따라 측정 값을 얼마나 반영시킬지 조절함

(z_k - H hat x_bar k)는 실제 측정값 - 예측 측정갑의 오차를 의미한다.

오차 공분산 행렬 예측값은 앞뒤로 시스템행렬 A를 곱해줘서 구한다.

오차 공분산 행렬은 예측 오차 공분산 행렬 - 칼만 이득 * 관측 행렬 * 예측 오차 공분산 행렬인데 P_bar k로 묶으면 아래와 같다.

오차 공분산은 추정 결과가 얼마나 올바른지 나타냄

결과가 올바르면 오차 공분산 행렬은 작아짐

말이 많이 지저분해졌는데 대충 정리하면

칼만 필터는 필터링, 상태 추정하는 필터

관측 값과 예측 관측 값의 차이(실 상태 값과 예측 상태 추정치 차이) 에 따라 칼만 게인을 조절해서

관측 값을 얼마나 반영시킬지 조정함

쓰고 보니까 원서에서는

prediction, correction이라 해서

이전엔 예측과 갱신이라고 표현했던거같은데

이미 이렇게 쓴거 그냥 나둠

대충 로직 설명은 여기까지가고 구현 들어감

데이터는 지난번에 만든 전압 데이터 사용ㅇ

import numpy as np

def get_volt():
    w = 0 + 4 * np.random.normal()
    z = 14.4 + w
    return z

for _ in range(10):
    print(get_volt())

지금 사용하는 상태는 전압 v 하나뿐이라

A H Q R P에서 행렬이라고 할게 없음

측정 노이즈 R 같은 경우에는

갯 볼티지 함수에서 4 * 정규분포(0, 1)을 해가지구

R을 4로 줌

x는 볼티지 기저 값을 14.4로 해서 14로 주고

A, H는 변환 할게 없이 그대로 쓰므로 1

시스템 노이즈 Q는 뭐라할게 없어서 0

추정하는 상태값이 볼트 1개 뿐이라 뭔가 하는것같은 느낌은 안들지만 

동작은 잘되긴 한다.

import matplotlib.pyplot as plt
A = 1
H = 1
Q = 0
R = 4
x = 14
P = 6
def kf(x, P, z):
    x_pred = A * x
    P_pred = A * P * A + Q
    K = P_pred * H / (H * P_pred * H + R)
    x_est = x_pred + K * (z - H * x_pred)
    P_est = P_pred - K * H * P_pred
    return x_est, P_est
t_list = np.arange(0, 10, 0.2)
volt_list = []
kf_list = []
x_est = 0
for _ in range(len(t_list)):
    volt = get_volt()
    if x_est == 0:
        x_est = x
        P_est = P
    x_est, P_est = kf(x_est, P_est, volt)
    volt_list.append(volt)
    kf_list.append(x_est)
plt.plot(t_list, volt_list, label="measurement")
plt.plot(t_list, kf_list, label="filter estimates")
plt.legend()

이번엔 소나 데이터로 저주파 통과 필터 만듬

내용은 단순하다

x_k = alpha * x_k-1 + (1 - alpha) * x_k

평균 이동 필터가 새로 들어온 값을 1/n 만큼 반영하다보니

필터 결과가 뒤쳐짐

저주파 통고가 필터에서는 alpha를 설정해줘서 1/n만큼이 아닌

위의 경우 (1 - alpha) 만큼 반영시켜서 좀 반응이 빠름

이전에 구현한 소나 데이터 로드함수 그대로 쓰고

import scipy.io

sonar = scipy.io.loadmat("SonarAlt.mat")

def get_sonar():
    sonar_arr = sonar["sonarAlt"][0]
    sonar_len = len(sonar_arr)
    for i in range(sonar_len):
        yield sonar_arr[i]

for val in get_sonar():
    print(val)

매트랩 코드 보니 조금 다른데?

그냥 이동 평균 구현한거 고쳐서 만듬

avg 계산은 없고 그대로 쓴다.

이건 아닌거가아서 이동 평균 구현한걸 lpf로 만들어버림

구현은 했는데 위에 이동 평균이랑 별 차이를 모르겠다 이동평균이랑 lpf랑 같이 섞어봄

import matplotlib.pyplot as plt

def lpf_filter(buf_list, alpha):
    prev_avg = sum(buf_list[:-1]) / len(buf_list[:-1])
    avg = prev_avg * alpha +  (1 - alpha) * buf_list[-1]
    return avg


idx_list, buf_list, val_list, avg_list = [], [], [], []
buf_len = 10
alpha = 0.7


for idx, val in enumerate(get_sonar()):
    if idx > 500:
        break
    buf_list.append(val)
    if len(buf_list) > buf_len:
        buf_list = buf_list[1:]
        avg = lpf_filter(buf_list, alpha)
        idx_list.append(idx)
        val_list.append(val)
        avg_list.append(avg)

plt.plot(idx_list, val_list, label="raw val")
plt.plot(idx_list, avg_list, label="filtered val")

alpha 값을 0.9로 했을때는 

이동 평균이랑 별 차이가 없었음 

alpha를 0.3으로 지정해서 새 값이 0.7만큼 가중을 시켰을때

실제 데이터에 좀 더 가깝고 반응이 빨랏음

500까지 하면 너무 새밀해서

200으로 샘플을 줄여 플로팅

import matplotlib.pyplot as plt

def lpf_filter(buf_list, alpha):
    prev_avg = sum(buf_list[:-1]) / len(buf_list[:-1])
    avg = prev_avg * alpha +  (1 - alpha) * buf_list[-1]
    return avg

def mov_avg_filter(buf_list):
    avg = sum(buf_list) / len(buf_list)
    return avg


idx_list, buf_list, val_list, lpf_list, mov_avg_list = [], [], [], [], []
buf_len = 10
alpha = 0.3


for idx, val in enumerate(get_sonar()):
    if idx > 200:
        break
    buf_list.append(val)
    if len(buf_list) > buf_len:
        buf_list = buf_list[1:]
        lpf = lpf_filter(buf_list, alpha)
        mov_avg = mov_avg_filter(buf_list)
        idx_list.append(idx)
        val_list.append(val)
        lpf_list.append(lpf)
        mov_avg_list.append(mov_avg)

plt.plot(idx_list, val_list, label="raw val")
plt.plot(idx_list, lpf_list, label="lpf val")
plt.plot(idx_list, mov_avg_list, label="mov avg val")
plt.legend()

이번에는 평균 이동 필터를 파이썬으로 구현하려고한다.

근데 여기서 이용하는 소나 데이터가 메트랩 확장자로 되어있다.

찾아보니까 사이파이쓰면 된다칸다

1. mat file 소나 데이터 읽기

sicpy io loadmat으로 mat 읽고

yield로 데이터 뽑아내도록 구현함

import scipy.io

sonar = scipy.io.loadmat("SonarAlt.mat")

def get_sonar():
    sonar_arr = sonar["sonarAlt"][0]
    sonar_len = len(sonar_arr)
    for i in range(sonar_len):
        yield sonar_arr[i]

for val in get_sonar():
    print(val)

2, 평균 필터 구현하기

대충 버퍼 사이즈 5라 치자

avg x_k = (x_k-4 + x_k-3 + x_k-2 + x_k-1 + x_k) / 5

avg x_k-1 같은 경우

= (x_k-4-1 + x_k-3-1 + x_k-2-1 + x_k-1-1 + x_k-1) / 5

= (x_k-5 + x_k-4 + x_k-3 + x_k-2 + x_k-1) / 5

이다 

avg x_k - avg x_k-1 로 우항 정리하면

= (x_k - x_k-5) / 5임

avg x_k = avg x_k-1 + (x_k - x_k-5) / 5

가 된다.

버퍼 사이즈를 5대신 n으로 놓자

avg x_k = avg x_k-1 + (x_k - x_k-n) / n다

다시 말을 정리하면

지금 x 평균 = 한번 전 x 평균 + (지금 x 값 + n번 전 x 평균) / n

근대 생각해보니까 파이썬에선 리스트 조절만하면 되지 이럴 필요가 없잔아--

위 내용은 무시해도 되고 

버퍼 사이즈 10 채운 상태서 평균 계산

다음 시간에선 오래된 값비우고, 새값 넣기 -> 평균계산

으로 루프 돌리면 된다.

대충 평균 이동필터 구현하긴 했는데

좀 지저분하게 만들어서 찜찜하다

idx 는 x축

x_list는 평균 필터 버퍼 리스트

xsaved는 소나 값 전체 모음

avg 는 평균 값 전체 모음 리스트

동작은 맞으니 pass

import matplotlib.pyplot as plt
def mov_avg_filter(x_list):
    avg = sum(x_list) / len(x_list)
    return avg
idx_list, x_list, xsaved_list, avg_list = [], [], [], []
buf_len = 10
for idx, val in enumerate(get_sonar()):
    if idx > 500:
        break
    idx_list.append(idx)
    x_list.append(val)
    xsaved_list.append(val)
    if len(x_list) < buf_len:
        avg_list.append(val)
    else:
        if len(x_list) > buf_len:
            x_list = x_list[1:]
        avg = mov_avg_filter(x_list)
        avg_list.append(avg)
plt.plot(idx_list, xsaved_list, label="sonar val")
plt.plot(idx_list, avg_list, label="filtered val")
plt.legend()

칼만필터는 어렵지않아

내가 이 책을 봤던게 19년도 쯤이었던거 같은데

그때 정말 설명을 너무 친절하게 해주셔서 감탄하면서 봤었다

당시엔 matlab있으니까 그냥했는데

지금은 메트랩이 없엉

또 2판이 새로나오면서 파티클필터도 추가되기도 했고

이참에 파이썬으로 작성해봐야되겟다 싶엇는데 구현하게 됨

1. 볼트 값 가져오기

평균 필터 파트의 get volt는

직류분 14.4에다가

정규분포 노이즈로 4 *  randn 사용

파이썬으로 구현하면 이럼

import numpy as np

def get_volt():
    w = 0 + 4 * np.random.normal()
    z = 14.4 + w
    return z

print(get_volt())

2. 평균 필터와 테스트 로직 구현하기

메트랩 코드를 파이썬으로 만들다보니

persistent 때매 좀 지저분 해지긴했지만 동작은 잘된다

import matplotlib.pyplot as plt
def avg_filter(prev_avg, k, x):

    if prev_avg == 0:
        return x, 1
    alpha = (k - 1) / k
    avg = alpha * prev_avg + (1 - alpha) * x
    k = k + 1
    return avg, k
t = np.arange(0, 10, 0.2)
sample_num = len(t)
avg_list, xm_list = [], []
prev_avg, k = 0, 0
for _ in range(sample_num):
    xm = get_volt()
    xm_list.append(xm)

    avg, k = avg_filter(prev_avg, k, xm)
    prev_avg = avg
    avg_list.append(avg)
plt.plot(t, xm_list, color="red", label="voltage")
plt.plot(t, avg_list, color="blue", label="filtered voltage")
plt.legend()