깜지로 쓰려는 블로그

테일러 급수를 이용한 근사

- 다항식 차수가 높아 질수록 더 넓은 범위로 근사값이 가까워 진다!

 => 테일러 급수는 연속미분가능함수를 n차 다항식으로 만들어 줄수 있음

  => n -> inf가 될때 얼마나 f(x)와 일치할까? 함수열의 수렴을 보아야함

- ln(1 + x)를 테일러 급수로 근사화한 모습

- 지수함수 y = e^x를 테일러 급수로 근사한 모습

점멸수렴과 균등 수렴

- 점멸 수렴 : 구간 I의 함수열 fn(x)들이, 구간 I의 점 x0에 f(x)로 수렴하는 경우.

- 균등 수렴 : 함수열 fn(x) - f(x)의 차이 상한이 0으로 수렴하는 경우

무한급수와 함수항 급수, 정급수

- 함수열 급수 : 함수열로 구성된 함수열

 ex) 함수열 u_n(x)로 f_n(x)를 정의한 경우

- 무한 급수와 함수항 급수 차이 : 무한 급수의 각 값이 값 대신 함수인 경우

- 정 급수 : 다음의 모습을 띄는 함수항 급수, x0은 정급수의 중심 

해석함수, 테일러 전개, 메클로린 전개

- 수렴 반경 :정급수 f(x)가 x0로부터 수렴할수있게 하는 범위

- 해석 함수 : 수렴 반경 r > 0인 정급수 f(x)가 임의의 점 x0에 대해 표현할 수 있는 경우 f(x)는 해석함수

 (= 테일러 전개)

- 메클로린 전개 : 테일러 전개에서 x0 = 0인 경우

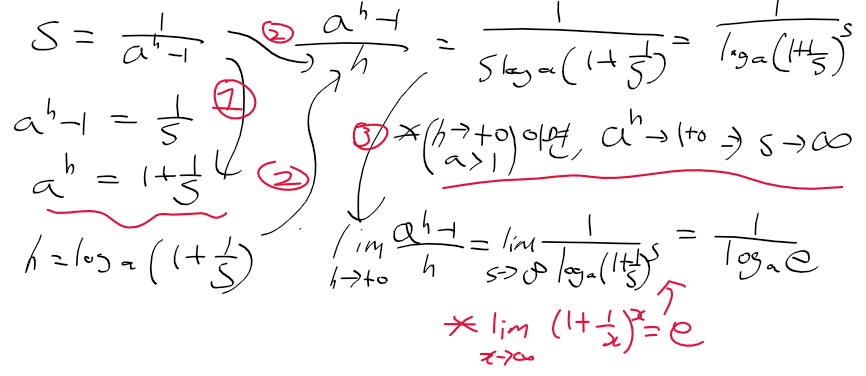
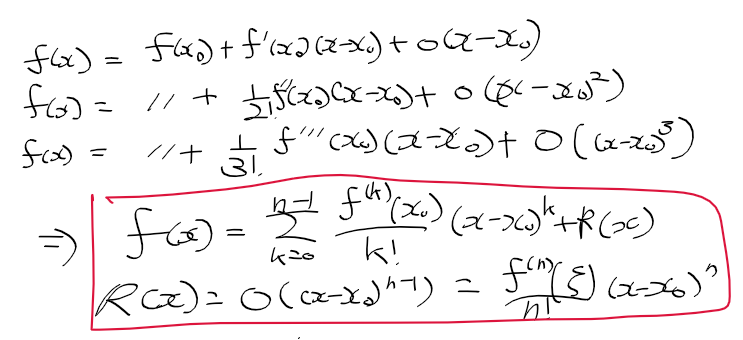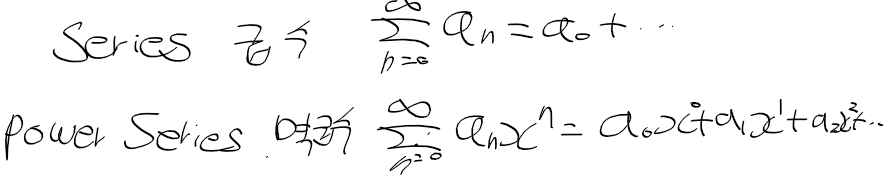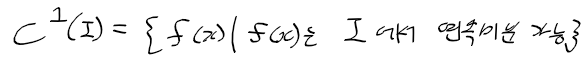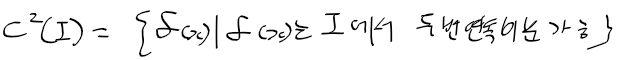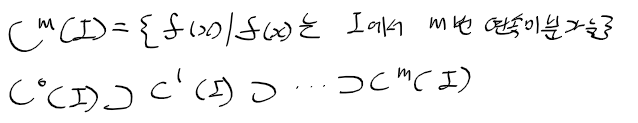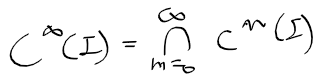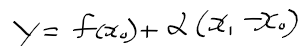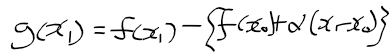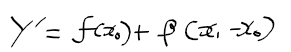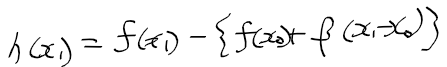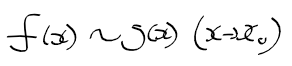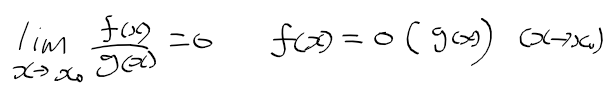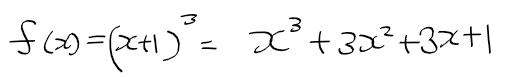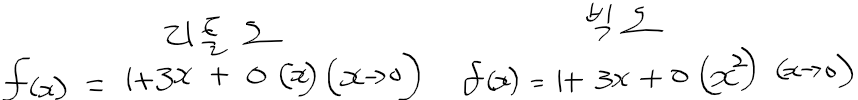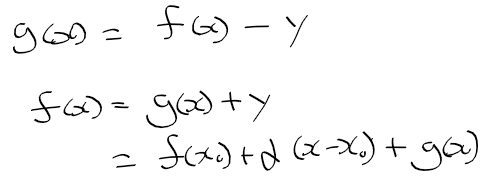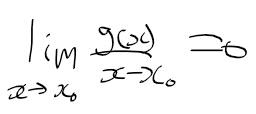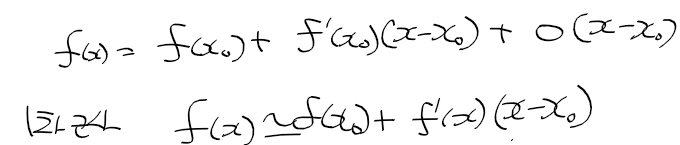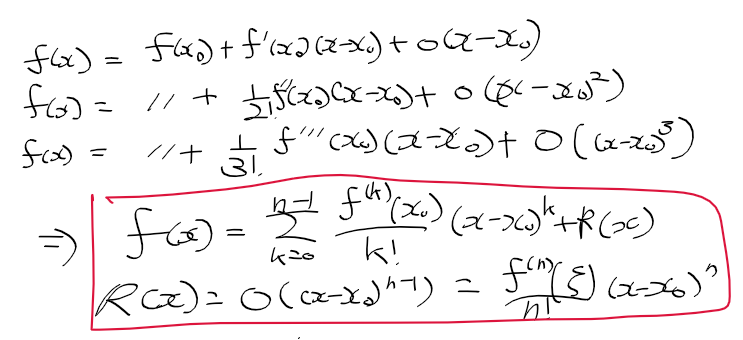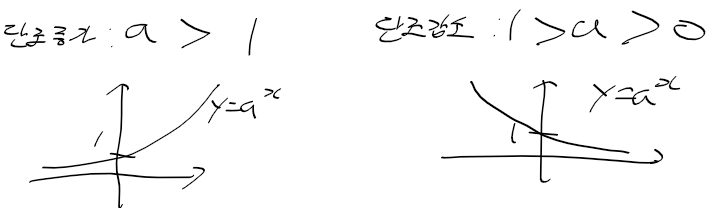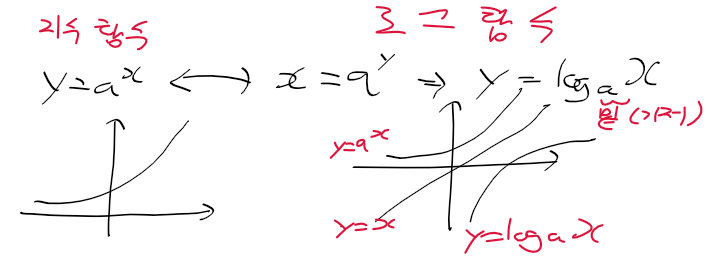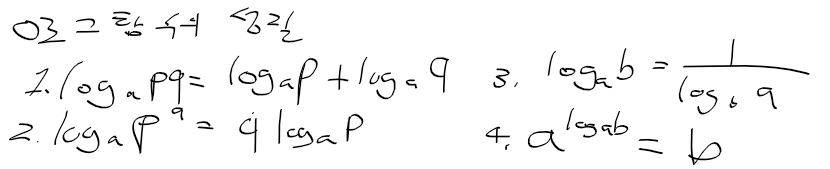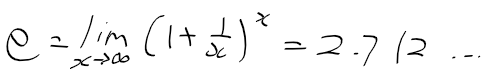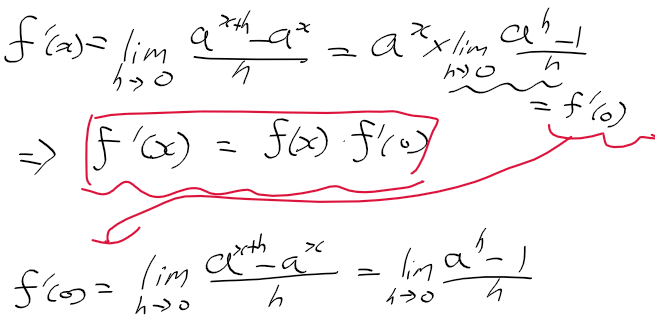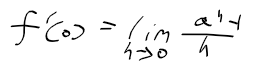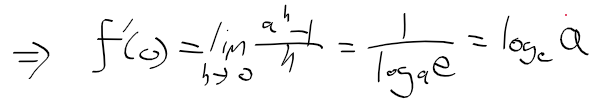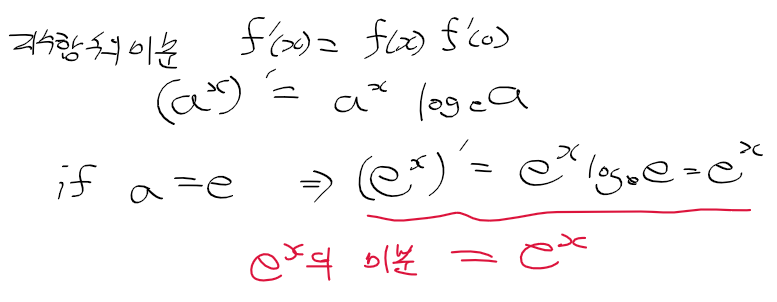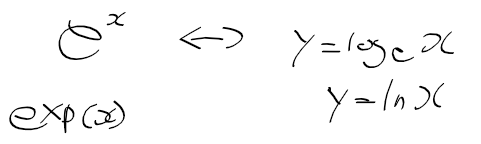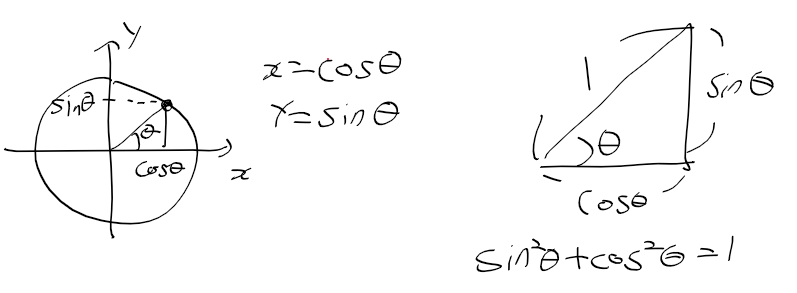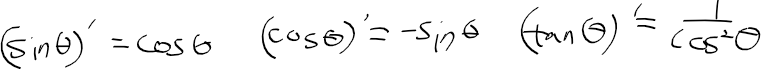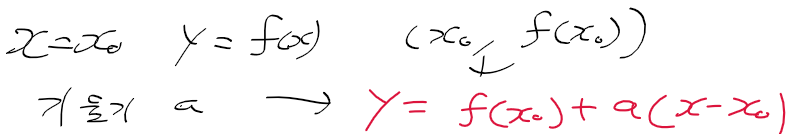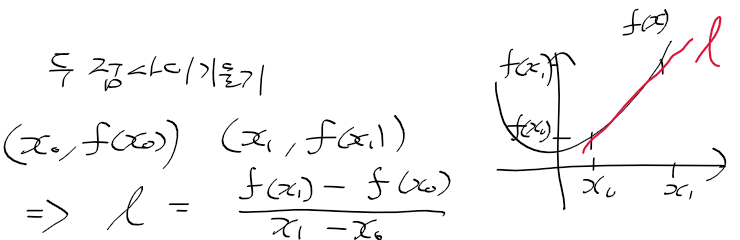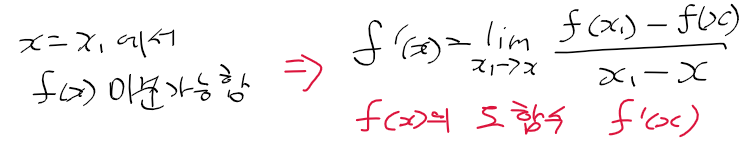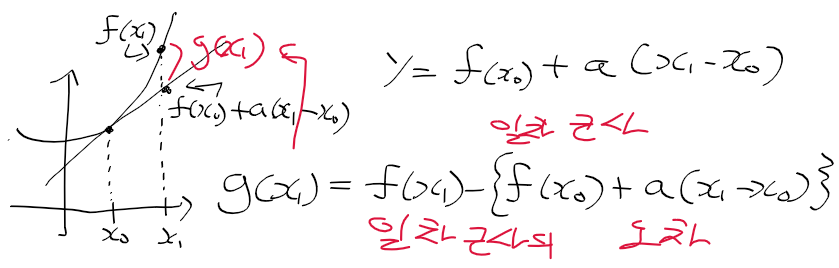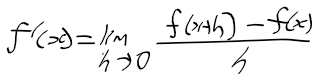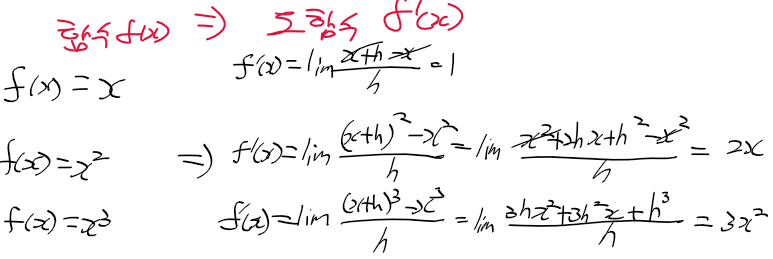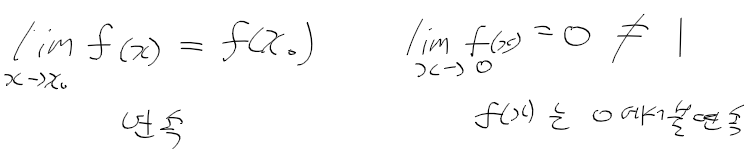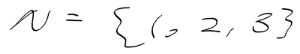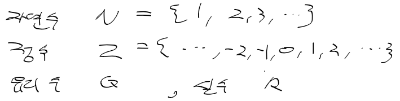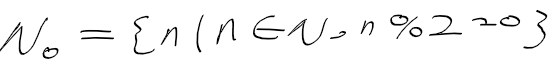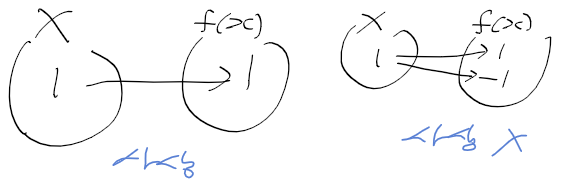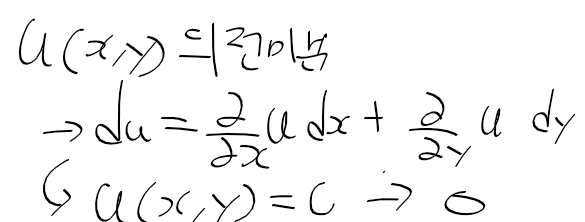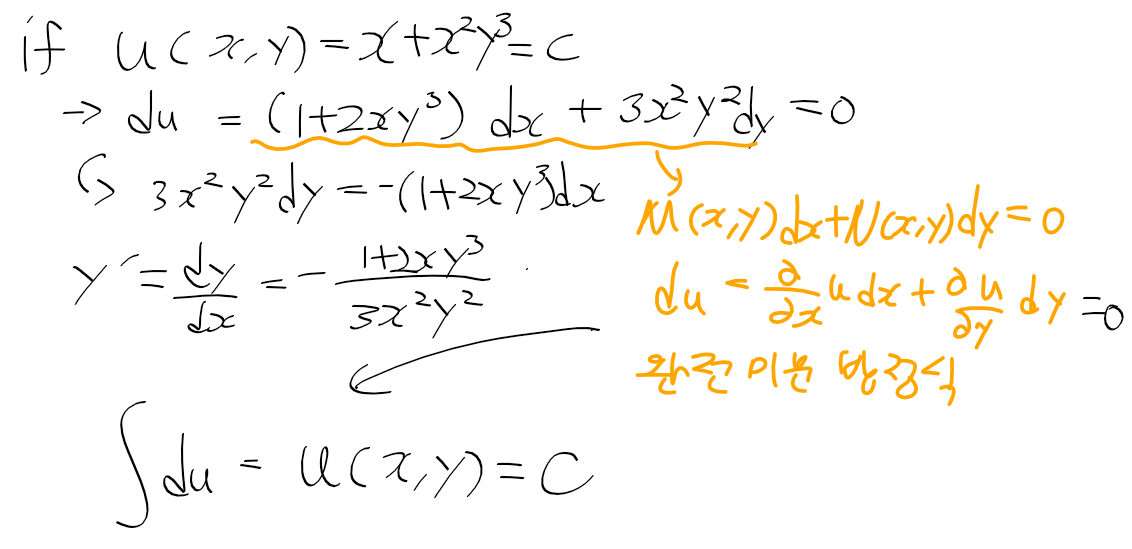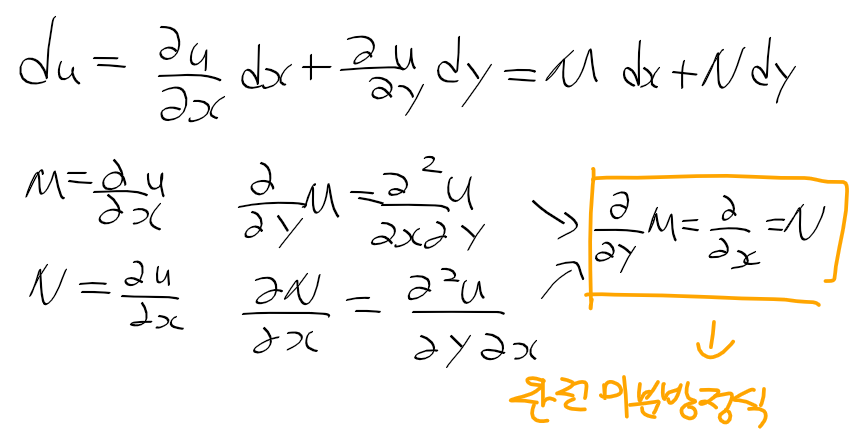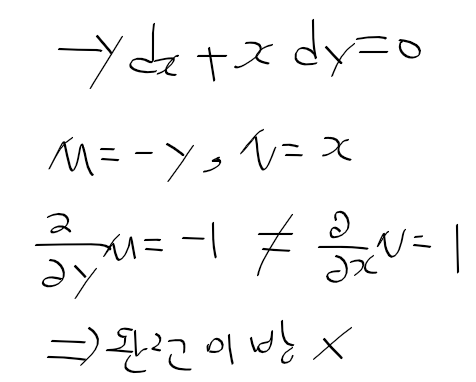멱급수

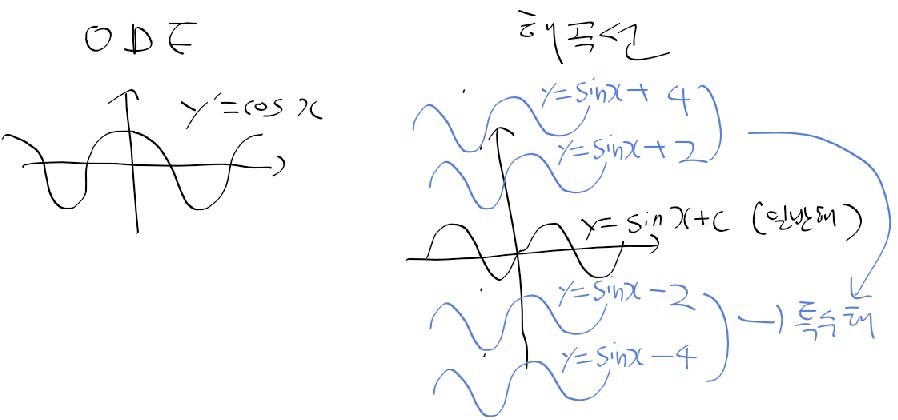
- 급수 : 수열의 합(유한급수 : 수열이 유한, 무한급수 : 수열이 무한)

- 멱급수 : 거듭제곱을 포함한 무한 급수

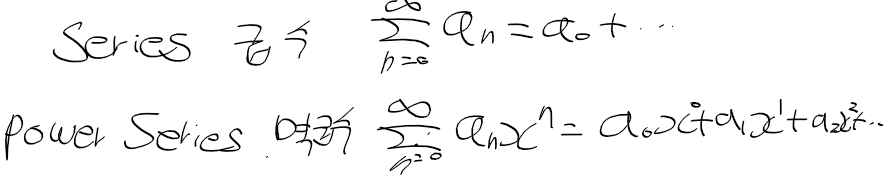
미분가능한 함수

- 연속미분가능 : 구간 I의 모든 점 x에서 미분 가능한 함수 f(x)는 다른말로 연속미분가능함

 -> I에 미분가능한 모든 함수의 집합 C^1(I)는 다음과 같음(C1-급 함수)

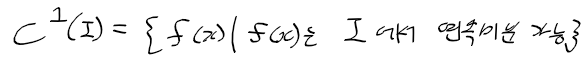
- 두번연속미분가능 : 도함수 f'(x)도 구간 I에서 미분 가능한 경우

 -> I에서 두번미분가능한 모든함수의 집합 C^2(I)는 다음과 같음

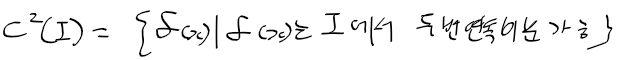
- m번 연속미분가능한 함수(m계 도함수)들의 집합을 다음과 같이 표현 가능하며 C 1 ~ m급 함수 집합은 다음 관계를 가짐

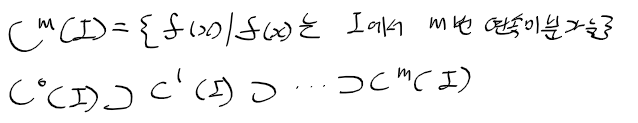
- 이런 집합의 교집합은 다음과 같음

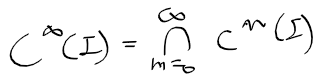
- 무한번 미분가능 함수 : C^inf-급 함수

일차 근사 되돌아보기

-  함수 f(x)를 x0에서 선형 근사한 일차함수가 (x1, f(x1))을 지나갈때 값 y는 다음과 같음(x0에서 미분계수는 alpha)

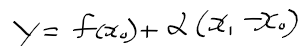
- 실제 f(x1)의 값과 일차 근사함수의 x1에서 값 차이를 g(x1)이라 하면 다음과 같음

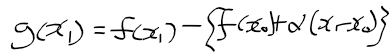
- 미분계수 alpha 대신 beta를 기울기로하고, (x1, f(x1))을 지나는 일차 함수 식은 다음과 같음

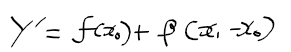
- 실제 f(x1)과 beta를 사용한 일차 함수 식의 값 차이를 h(x1)이라 하면 다음과 같다.

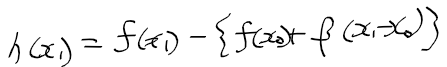
- 함수 f(x), g(x1), h(x1)의 관계는 다음과 같음

 => x1->x0으로 극한에서 g(x1)이 h(x1)보다 오차가 작음

  => x1 -> x0이 되어갈수록 g(x1)이 h(x1)보다 빠르게 0에 가까워진다!

   => alpha = f'(x0)이 최적의 1차 근사이다! 

   (beta를 기울기로 하는 선형 근사는 오차가 더 크므로)

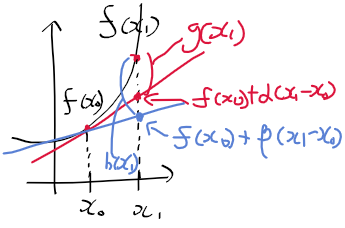
무한소

- 무한소 개념

 1) 모든 양수보다 작지만 0보다 큰 상태

 2) 엡실론델타논법 존재전에 극한을 설명하기 위해 고안한 개념.

 3) x->x0에서 무한소란? : x -> x0 극한에서 0 되는 함수f(x)

- 아래 g(x), h(x), g(x)/h(x)의 x->0 일때 값의 변화

  => g(x) = x^2가 가장 빠르게 0에 근접한다!

- 비교 가능 무한소 : 위 g(x), h(x)와 같이 특정한 값에 수렴하는 경우의 함수

- 동위 무한소 : 아래의 식에서 alpha != 0 인 경우

- 동치 무한소 : 위의 식에서 alpha = 1인경우, 동치관계라고도 함. 아래와 같이 두 함수사이 물결로 표현

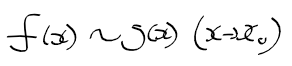
- 동위와 동치 무한소 : 동치무한소는 0에 수렴하는 속도가 같다! 동위 무한소는 수렴 속도가 상수배 다르다

- 무시가능 무한소 : 좌측 식처럼  f(x)가 g(x)보다 빨리 0에 수렴(분자가 먼저 0된다)하는 경우 f(x)는 g(x)의 무시가능무한소

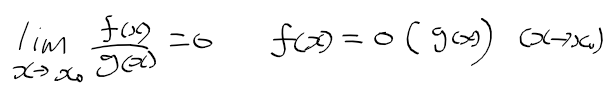
무시가능 무한소와 근사식

- f(x) = (x + 1) ^3, g(x) = x로 놓고 전개해보자

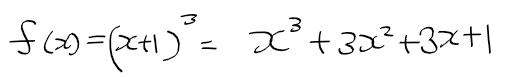
- lim f(x)/g(x) = 0을 성립시키기위해 f(x) - (1 + 3x)를 분자, g(x)=x를 넣으면 다음과 같이 정리된다.

- 즉 f(x) - (1+3x) = o(x)      

  => x가 0에 가까워질 때 "f(x) - (1+3x)"는 x의 무시가능 무한소 o(x)가 된다.

  * 이때 o(x) = x^3 + x^2로 1차보다 높은 항만으로 구성됨.

- o(x)를 제외하고 f(x)에 대한 식으로 정리하면, x가 0에 가까워질때 3x + 1란 1차 근사식이 나온다.

란다우 기호

- 위 식에서 무시가능무한소 o(x)에서 사용한 기호 o 혹은 O

- 리틀오 : o는 x보다 큰 차수 항들의 모임

- 빅오 : O(x)는 x를 포함하여 x보다 큰 차수 항들의 모임

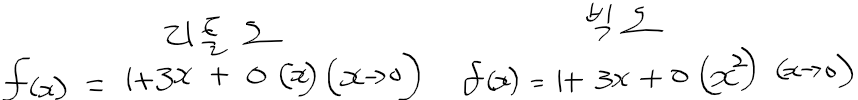
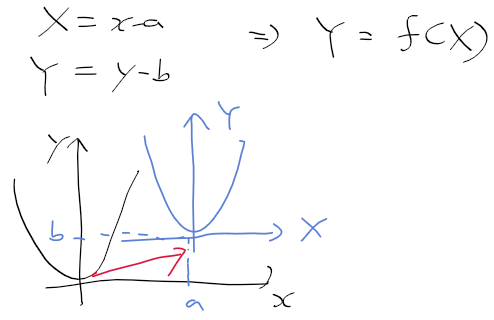
란다우 기호로 1차 근사 표현하기

- 아까 일차 근사 되돌아보기에서 그린 그래프를 다시 가져와서 보자

- x0 직선의 방정식에 x1을 대입하지 않고 x에 대한 식으로 나두면 다음과 같다

- 그러면 f(x)와 직선 방정식(대충 y라 하자)의 오차를 g(x)라 하였으므로, f(x)는 다음과 같이 정리할수 있다.

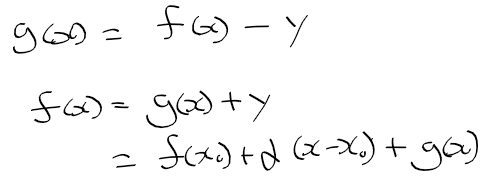
 - 이 때 g(x)는 x-x0의 관계를 다음과 같이 정리할수 있다. 즉, g(x)는 "x-x0"에 대해 무시가능무한소 

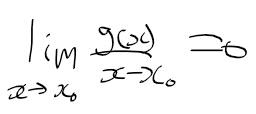
- f(x)를 란다우기호로 다시 정리하면 다음과 같이 되며 1차 근사로 다시 정리할수있다.

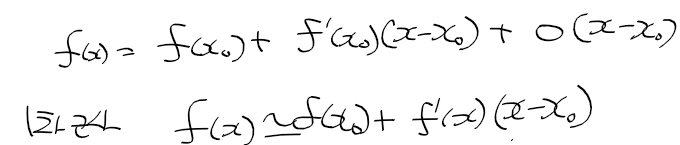
테일러 공식과 f(x)

- 테일러 공식으로 f(x)를 정리하면 다음과 같음

 * 테일러 공식 : 폐구간 [x, x0]에서 f^(n-1) (x)가 연속이고 f^(n)이 존재시 다음 관계가 성립

초등함수

- 다항함수, 지수함수, 로그함수 및 함수의 합성과 사칙연산으로 구할  수 있는 모든 함수

- (주의) 초월함수 : 대수적으로 구할수 없는 함수. 초월함수와 초등함수는 항상 같지 않음

  * 지수함수, 로그함수, 삼각함수는 초등함수이면서 초월함수이기도 함(?)

  => 테일러 급수로 구할수 있어서 이들이 초등함수와 초월함수 둘다 포함되는건지 잘 모르겠음

지수 함수

- 양의 상수 a( a > 0)이 주어질때 y = a^x인 함수

 * 여기서 a가 왜 양수인 경우만 다루는지는 잘 모르겠음

단조 증가와 단조 감소

- 지수함수는 a > 1인지 1 > a > 0 인지 여부에 따라 단조 증가, 단조 감소의 형태를 보임

- 추가로 지수 함수는 실수 전체에 정의되어 단조증가, 단조증가하나 치역(y 범위)는 양의 실수 공간임

로그 함수

- 지수 함수를 역으로 하면 x = a^y를 만족하는 역함수가 존재함

- 로그 함수 : a를 밑(기저)로 하는 지수함수의 역함수

로그함수의 성질

- 로그 함수는 복잡한 곱샘 나눗셈을 단순한 덧셈, 뺄셈으로 변환해준다!

네이피어의 수

- 1에 가까워지는 1 + 1/x를 무한에 가까워지도록 x번 곱하면 (1 + 1/x)^x 했을때 수렴하는 수

- e = 2.712...

지수함수의 미분

- 도함수의 정의에 지수함수 f(x) = a^x를 대입하면 다음과 같이 지수함수의 도함수를 구할 수 있음

 * 갑자기 f'(0)가 나오는 이유는 지수함수의 도함수식 x에다가 0을 대입하면 그대로 나오기 때문

밑이 e인 지수함수의 미분이 자기자신인 이유

- 먼저 f'(0)에서 시작하자

- 1) s = 1/(a^h - 1)를 정리하면 a^h = 1 + 1/s이 나온다. 이를 h에 대한 식으로 정리하자

- 2) s와 h에 대한 식을 f'(0)에 대입한다

- 3) f'(0) = 1/log_a_e가 나온다

- 그러므로 지수함수 f(x)의 f'(0)는 log_e_a가 된다.

 - 지수함수의 도함수 정리 결과에 a=e와 f'(0) = log_e_a를 대입하면 (e^x)' = e^x가 나온다

밑이 e인 지수함수와 역함수(자연로그)

- 지수함수의 역함수가 로그함수 이듯, 밑이 e인 지수함수의 경우에도 역함수는 로그

- 밑이 e인 로그함수를 자연로그라 부르며 ln x로 표기

- 밑이 e인 지수함수는 exp(x)로 표기

삼각함수와 도함수

- 반지름 길이가 1인 단위원과 0<= theta <= 2pi에서 x, y의 좌표

- 피타고라스 정리와 삼각함수 : cos^2 theta + sin^2 theta = 1

- 탄젠트 = 사인 / 코사인

- 삼각함수의 도함수 정리 하기 귀찬으므로 결과만 놓으면...

한 점을 지나는 접선의 방정식

- x0에서 연속인 함수 f(x)의 접선인 (기울기 a) 방정식은 다음과 같음

두 점을 지나는 직선의 기울기

- y = f(x)의 두 점 x0, x1을 지나는 직선의 기울기는 다음과 같다

극한을 통한 접선의 기울기

- 위에서는 두 점을 지나는 직선의 기울기를 구함

- x1이 x0에 점점 가까워지면 x0에서의 점선에 대한 기울기가 나온다.

램프 함수의 기울기는?

- 자주 사용하는 램프 함수는 x가 0미만에서는 0이고, 0이상에서는 x이다. 그러면 램프 함수의 기울기는 어떨까

 => 램프 함수는 0에서 좌극한과 우극한이 다르므로 미분가능하지 않음

도함수

- 함수 f(x)의 한 점에서 기울기를 구하는 식 f'(x)

- x = x1인 지점에서 f(x)가 미분가능한 경우 도함수 f'(x)는 다음과 같음

미분 계수와 도함수 차이

- 도함수 : 임의의 점 x에서 함수 y = f(x)의 접선 기울기를 구하는 식(x 미정)

- 미분 계수 : 특정한 x 지점에서의 기울기(x 지정)

미분 계수 표현하기

- 미분 계수 a는 dy/dx로 표현

- 미분 계수는 한 점에서의 기울기이므로 해당 지점은 다음과 같이 표현

일차 근사

- 근사식 : 주어진 함수 y = f(x)에 가깝게 근사/표현한 식

- 일차 근사 : 일차 함수(= 직선에 대한 함수)로 y = f(x)에 가깞게 나타낸 식

- 실제 값과 근사 값의 차이 : x1에서 실제 함수와 (x0에서 선형 근사한)일차 근사 함수에는 다음과 같이 차이가 존재

도함수와 미분의 의미와 도함수 예시

- 도함수 : 임의의 x에 대한 함수 y = f(x)의 접선 기울기를 구하는 식

- 미분 : f(x)의 도함수를 얻는 것

- 함수 f(x) = x, f(x) = x^2, f(x) = x^3 의 도함수 예시

정적분과 구분구적법

- 정적분 : 함수의 면적을 구하는 방법

- 구분구적법 : 폐구간 I = [a, b]의 연속함수 f(x)의 각 작은 구간에 대한 직사각형을 합하여 면적 근사 계산한 방법

원시함수와 부정적분

- 부정적분 : 임의의 적분 가능한 구간에서의 정적분 

- 원시함수 : F'(x) = f(x)를 만족하는 함수 F(x)

- 부정적분과 원시 함수의 관계 : 원시함수 = 부정적분 + 임의의 상수 C

함수의 평행 이동

- 가로축 x, 세로축 y로 놓는 함수 y = f(x), 를 x축에 대해서 a만큼 y축에 대해서 b만큼 평행 이동한다면

- X = x - a, Y = y - b로 놓는다면 x, y에 대한 함수가 아닌 X, Y에 대한 함수로 만들 수 있다.

합성 함수

- 여러 함수를 순서대로 적용하는 것

- x를 함수 f에 사상한 값 f(x)를 다른 함수 g로 사상한 값은 g(f(x))

* 주의 : f의 치역이 g의 정의역에 들어가야 함

- 다음의 경우 x는 임의의 실수 R이 아닌 [-1, 1]의 구간으로 정의역을 제한해야함

 1) g(x)는 음수가 존재 하지 않음

 2) f(x)는 최대가 1임

  => g(y)의 정의역은 [0, 1]

    => 이를 위함 f(x)의 정의역은 [-1, 1]

역함수

- y로 x를 구하는 역방향 함수, y=x로 뒤집은듯한 형태

- 함수와 역함수의 합성 함수는 항등 함수

* 주의 : f(x) = x^2의 경우 y=x로 뒤집을 시 하나의 x에 y가 2가지가 동시에 나옴

   => 정의역을 명확히 제한해야함

함수의 극한과 연속성

- 함수 f에서 x가 특정 값 x0에 가까워질때 f(x)가 a에 가까워지는 것

- 아래의 경우 x가 0에 가까워질때 lim f(x) = 0이나 f(0)=1이므로 불연속

이전부터 수치해석이나 최적화이론을 한번 봐야하겠다 생각은 하고있었지만

해석학이 뭔지도 잘 모르는 상태에서는 억지로 파려고 해봤자 소용없다는 생각밖에 들지 않았다.

최근에서야 수학사 관련한 책과 영상들을 보면서 해석학이 뭔지 기하학이 뭔지 이제야 감이 슬금슬금 잡힐랑 말랑하는데

전에는 구글링해서 나온 글들을 보며 해석학은 수식가지고 계산하는거고 수치해석의 수치적 방법은 정확하지는 않더라도 어느정도 정밀성을 가진 값을 찾아낸다. 정도의 이해밖에 하지 못하고 있었다.

아무튼 다시 수학 공부하기에 앞서 가장 기초가 되는 미적분학(해석학)의 복습 필요성을 느껴서 대충 대충 정리하더라도 다시 시작하려고한다.

집합

- 무언가의 모임

대표적인 집합의 기호

원소 x가 집합 A에 포함됨(x는 A의 원소이다.)

짝수의 집합

- 짝수의 집합 N0는 n으로 구성됨.

- n은 2로 나누어 얻은 나머지가 0인 수

=> N0는 짝수의 집합

집합에서의 사상

- 사상 : 두 집합의 원소 간 대응 관계/연결

  ** x = 1 => f(x) = 1 과 같은 대응관계

   하지만 x = 1인데 f(x) = 1  혹은 f(x) = -1 두가지 값이 나오는 경우는 존재하면 안됨.

- 정의역 : (사상의) 출발점 집합 

- 치역 : (사상의) 도착점 집합

- 단사 : 대응 관계의 목적지가 모두 다르다

- 전사 : 모든 대응 관계의 목적지가 연결된 경우 

- 전단사 : 대응 관계의 목적지가 모두 다르며, 연결되어 있는 경우

구간과 기호

- 폐구간 : 경계를 포함 [, ] 기호 사용

- 개구간 : 경계를 포함안함 (, ) 기호 사용

선형미분방정식과 비선형 미분방정식

- 선형미분방정식 : 도함수/종속변수가 1차인 미방

   * n계 선형미방 : 가장 많이 미분한 항이 n번 미분한 미방

- 비선형미분방정식 : 도함수/종속변수가 1차가 아닌 미방

선형 미방과 비선형 미방 비교

- 아래의 예시에서 첫번째 미방의 경우 다차항이없고, y''가 가장 많이 미분하였므로 2계 선형 미방

- 두번째 미방의 경우 (y')를 제곱하여 2차가 되므로 비선형 미방

1계 선형 상미방의 대수적 표현과 표준형

- 1계 선형 상미방 : 아래와 같이 다차항이 없는 1계 상미분방정식

 * 우항의 r(x)는 입력을 의미(ex: 힘, 전류, 변위 등)

 * y(x)는 입력에 대한 출력

-  y'의 계수가 f(x)일 때 f(x)를 나누어 아래와 같이 y'의 계수를 1로 만들었을때의 미방을 1계 선형 상미방의 표준형

동차와 비동차

- 아래와 같이 우항이 0인 선형미분방정식을 동차 선형미방이라 하고, 0이 아닌 경우를 비동차 선형미방이라 한다.

- 동차 선형 미분 방정식 : 모든 항이 y 혹은 y의 도함수를 가지고 있다.

- 비동차 선형 미분 방정식 : 모든 항이 y 혹은 y의 도함수를 가지고 있지는 않다.

동차 선형 미방과 자명해(trivial solution)

- 다음의 동차 선형 미방의 표준형을 변수 분리하고, 적분 한후, 지수함수를 취하면 아래의 일반해(동차해)를 얻음

- 이 일반해에 c = 0을 대입하면 해당 구간 모든 x에 확실한 자명해 y(x)=0이나옴

 * 자명해는 당연한 해로 필요 x

비동차 선형 미방의 해

- 아래의 비동차 선형 미방이 주어질때, 적분 인자 F를 곱하자

- pF = F'의 조건을 주고, 변수 분리법으로 분리한 후, 적분과 지수함수를 취한 결과 F = e^h가 나온다.

- 이를 Fy의 합성함수 미분 식에다가 대입한 결과. (Fy)' = r * F임을 얻는다.

- (Fy)'를 적분 후, 양변에 F(=e^h)를 나눈 결과 응답 y(x)에 대한 식이 나오며, 입력의 응답과 초기조건응답으로나뉜다.

ex1) 1계 선형 상미분방정식의 초기값이 주어질때 응답 y 구하기

- 아래의 미분방정식과 초기조건, y에 대한 식이 주어지면  입력 r = sin 2x, p = tanx

- h = p = tan x의 적분이며 e^h = sec x가 나온다. 이를 통해 식 y의 r*e^h와 e^-h를 구한다.

- 정리한 식 y에 초기조건을 대입한 결과 c = 3이 나왔으므로, 이 선형 미분 방정식의 특수해는 아래와 같다.

ex2) RL 회로의 전류를 구해보자

- RL 회로가 주어지면,  KVL과 옴의법칙을 통해 구한 1계 선형 상미분방정식과 그의 표준형은 다음과 같다

- 비동차 선형미방의 일반 해를 구해보자

- 초기조건 I(0) = 0  <= 인가 시작떄 전류가 0이다. 초기조건을 통해 특수해를 구하자

 * 회로이론의 RL회로 전류 인가시 전류의 과도응답 식과 같다! wow

베르누이 방정식(비선형 상미방을 선형 상미방으로 바꾸기)

- 베르누이 방정식 : 실제 많은 문제는 비선형 -> 선형 상미분으로 변환하면 쉽게 풀수 있있으며 이 방법 중 하나

- 아래의 식에서 우항 y의 차수가 0 or 1이면 선형이지만 그렇지 않으면 비선형 상미방이 된다.

- 아래의 u에 대한 식을 미분하고 y'를 대입하자. u에 대한 선형 상미방이 나온다!

변수분리법

- 다음과 같은 상미분 방정식(변수 분리 가능 방정식)이 주어질 때, 양변에 x로 적분을 하고 정리를 하면 좌변은 y만 우변은 x만 나오며 이를 계산하여 일반해를 얻는 방법

변수 분리법을 이용한 예제

편미분과 전미분

- 편미분 : 다변수 함수에서 한 변수만을 다루고 나머지 변수들은 상수로 취급한 미분 

 -> 한 변수가 변할때의 변화율

- 전미분 : 다변수 함수에서 모든 변수를 동시에 다루는 미분

 -> 모든 변수가 변할때의 변화율

전미분과 완전미분방정식

- 함수 u(x,y)의 편도함수가 연속일때 이 함수의 전미분은 다음가 같고, u(x, y)가 상수인 경우 전미분은 0이된다.

- u(x,y)가 아래와 같이 주어진 경우 전미분을 구하고, 미분방정식의 형태로 만들면 완전미분방정식이 나온다.

- 이 완전 미분방정식 du = 0이므로 적분을 하여 일반해를 구하면 u(x, y) = c의 형태로 음함수해가 된다.

완전미분방정식이 되기 위한 조건

- 완전미분방정식은 전미분 du = M(x, y)dx + N(x, y) dy 의 형태가 되야 하며 M과 N의 편도함수가 같을때 성립한다.

완전미분방정시 아닌 경우와 적분 인자

- 아래의 식은 완전 미분방정식이 되지 않음.

- 1/x^2을 곱할 시 

- 적분인자 : 방금 완전미방이 아닌 식에 1/x^2을 곱하여 완전미방으로 만든 것처럼 곱한 함수 F(x,y)가 적분인자.

미분 방정식 differential equation

- 현실의 물리 현상을 미분을 통해 모형화 한 방정식

- 상미분 방정식 ode ordinary de : 변수가 한개인 미방

- 편미분 방정식 pde partial de : 변수가 여러개인 미방

- 모델링 : 공학, 물리학, 화학 등 여러 분야의 실제 현상을 수학적으로 계산할 수 있도록 표현한 모델

* 목표 : 현실 문제에서상미분 방정식을 유도(모델링)하고, 방정식을 풀고 그래프 시각화하여 해석하자

1계 상미분 방정식

- 2차, 3차등 고차 도함수가 아닌 1차/1계 도함수만을 가지고 있는 미분방정식

공학 문제와 모델링

- 공학 문제를 계산을 통해 풀려면 수학 모델로 만들며 이를 모델링이라 함

- 모델링에 미방을 사용하는 이유 ? -> 다양한 물리 현상들이 도함수(미분)을 포함하고 있음(ex:속도, 가속도)

상미분방정식과 편미분 방정식

- 상미방 : 하나의 변수 <-> 편미방 : 여러 변수

미분 방정식 활용 예시

- 낙하, 스프링에서 변위, RLC 회로 전류, 진자 운동

상미분방정식의 양형태, 음형태

- 양형태 explicit form : 모든 항을 좌변으로 옮김

- 음형태 implicit from : 도함수만 좌변으로 옮김

해

- 해 : 어느 함수 h(x)가 열린 구간에서 정의/미분 가능하며, 이 함수 h(x)를 만족하는 y

- 해곡선 : 해들의 곡선

- 열린 구간 : a < x < b에서 양 끝 a와 b를 포함하지 않는 구간

상미분 방정식과 해

- y' = cos x인 (음형태) 상미분방정식이 있을때, ode의 해는 y = sin x + C

- 일반해 general solution : 임의의 상수 C를 가지고 있는 해

- 특수해 particular solution :  임의의 상수 C를 특정값으로 할때의 해

특수해와 초기값

- 초기조건 : 특정 입력값에 대한 출력 -> 일반해에 대입해 임의의 변수 c 값을 구할 수 있다.

 => 초기조건을 통해, 해당 초기조건의 특수해를 구한다.(초기값 문제)

초기값 문제 예시

- y' = 3y, y(0) = 5.7일 때 특수해를 구해보자

 * y' = 3y : y를 미분했더니 y가 나온다 y는 지수함수의 형태다.

 * 구한 일반해에 위 초기조건을 대입하여 C를 구하

=> 특수해 y = 5.7 e^3x

해석적 방법과 수치적 방법

- 해석적 방법 : 직접 계산하여 정확한 해를 구함

- 수치적 방법 : 근사화를 통해 해를 구함

1계 ode의 기하학적 의미

- y' = f(x, y)를 기하학적으로 해석해보자

- 점 (x0, y0)을 지나는 위 ode의 해곡선은 y'(x0) = f(x0, y0)을 만족해야한다.

 -> 그래픽 or 수치해석적 방법으로 ode의 근사해를 얻을 수 있다.

상미분 방정식의 방향장 시각화

- y' = y + x라는 상미분 방정식이 주어질 때, (0, 1), (0, 0), (0, -1) 세 점을 지난다면

 -> 3개의 해곡선을 가지며, 세 해곡선과 해당 ode의 방향장은 다음과 같다.

* 뒤에 오일러방법 계산하다가 자꾸 값이 이상하게 나왔는데 일반해부터 잘못 구한거같다

오일러 방법 - 간단한 수치해석적 방법

- ode와 초기값이 주어질 때, x1 = x0 + h라면

  => y1 = y0 + h * y' = y0 + h * f(x0, x0)

- 간격 h가 작을수록 오차는 줄어든다.

- h = 0.2로 놓고 구한 근사값과 실제 특이해를 비교하면 오차가 점점 커지는걸볼수있다.