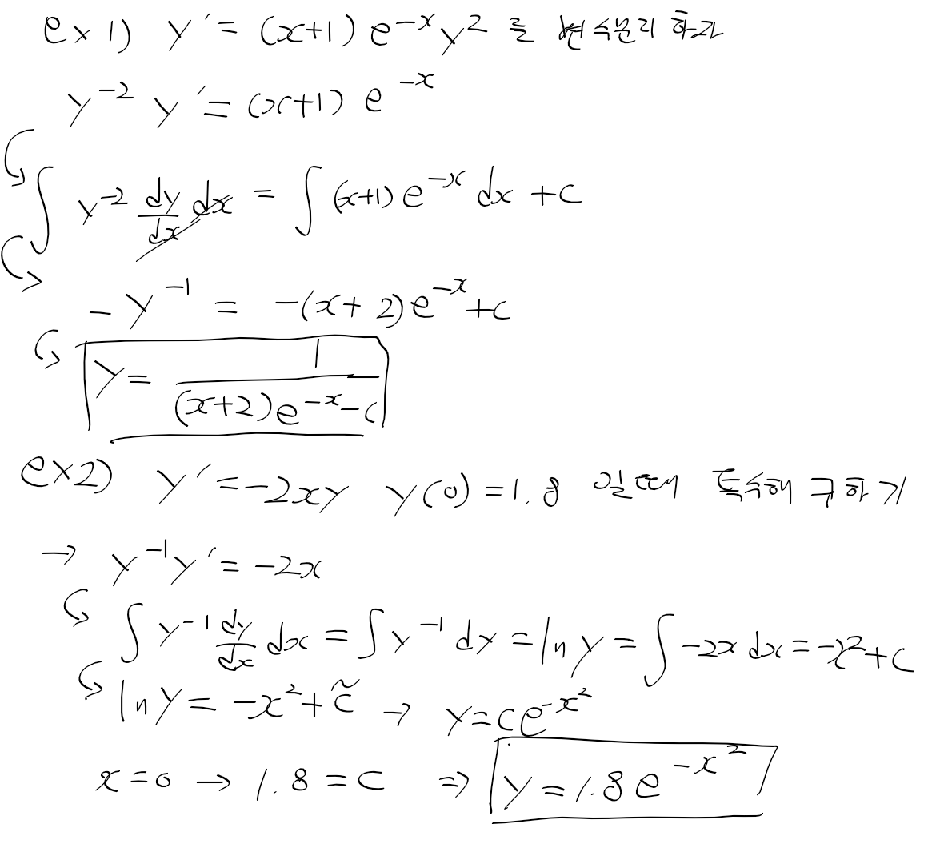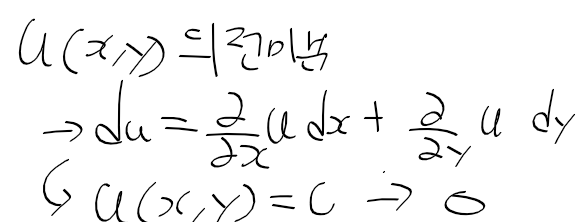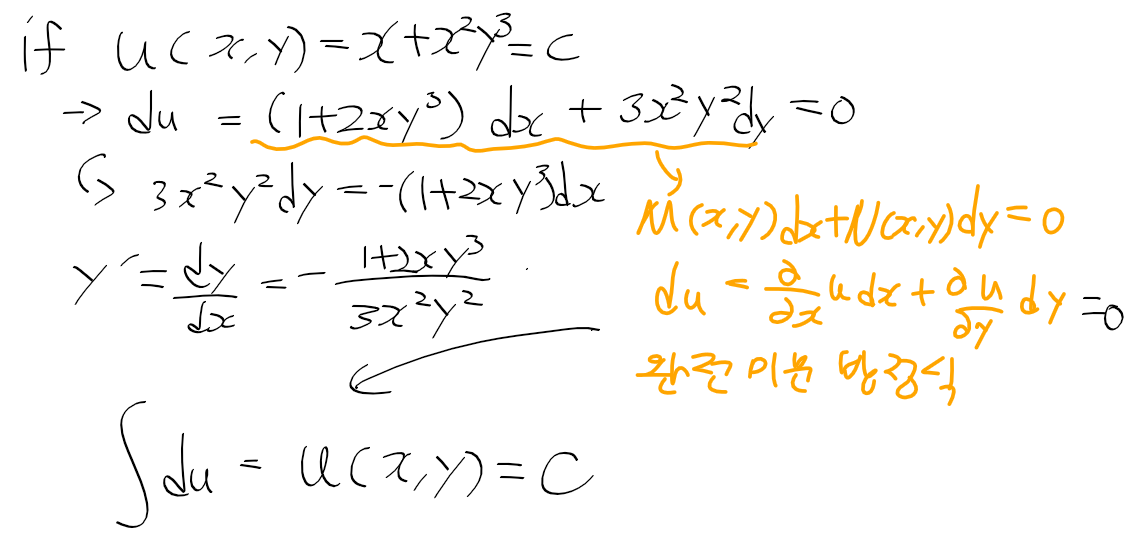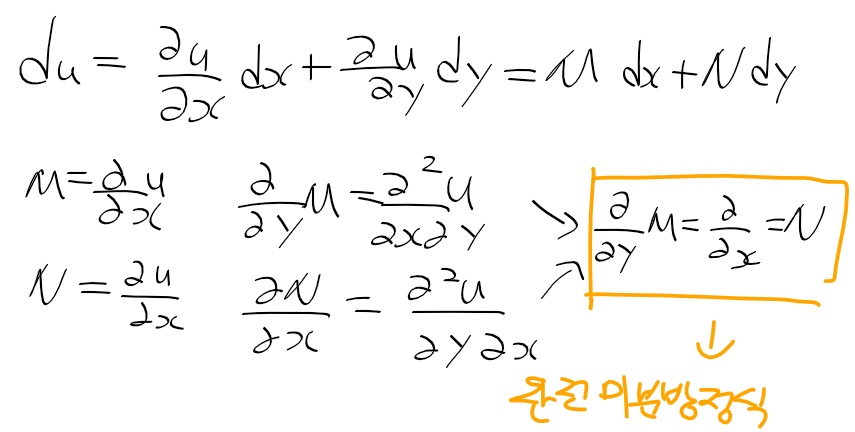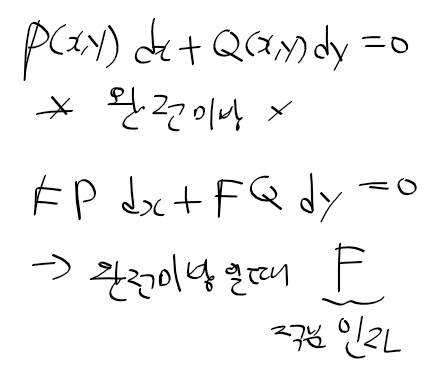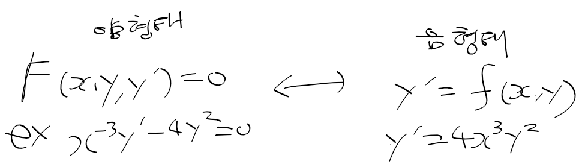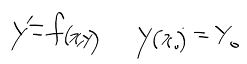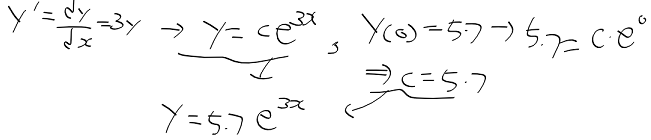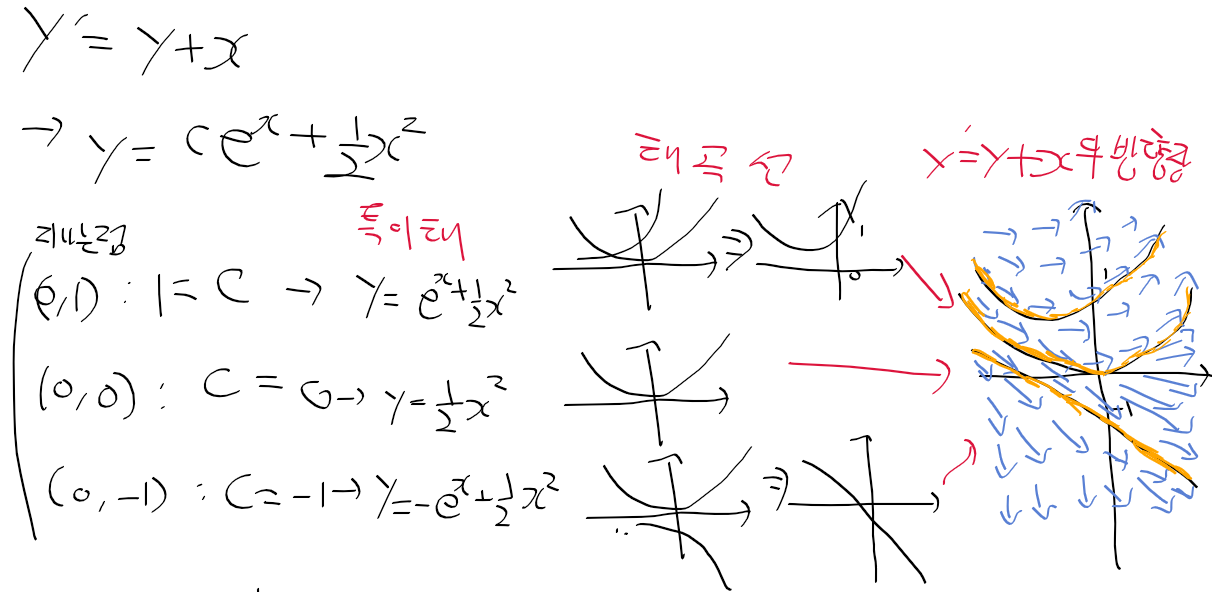선형미분방정식과 비선형 미분방정식
- 선형미분방정식 : 도함수/종속변수가 1차인 미방
* n계 선형미방 : 가장 많이 미분한 항이 n번 미분한 미방
- 비선형미분방정식 : 도함수/종속변수가 1차가 아닌 미방
선형 미방과 비선형 미방 비교
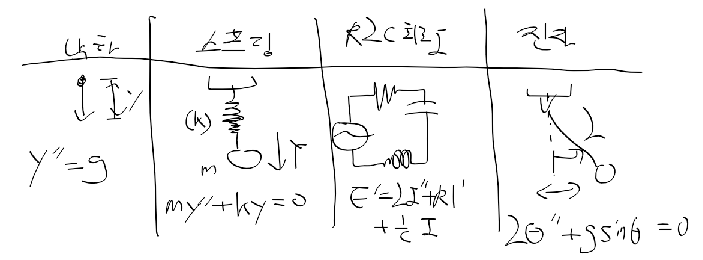
- 아래의 예시에서 첫번째 미방의 경우 다차항이없고, y''가 가장 많이 미분하였므로 2계 선형 미방
- 두번째 미방의 경우 (y')를 제곱하여 2차가 되므로 비선형 미방
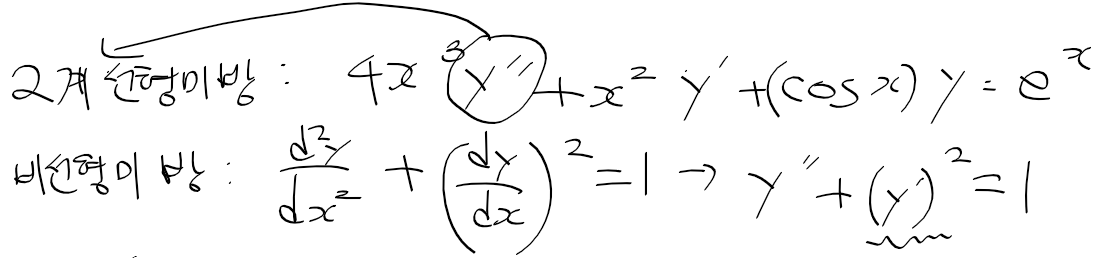
1계 선형 상미방의 대수적 표현과 표준형
- 1계 선형 상미방 : 아래와 같이 다차항이 없는 1계 상미분방정식
* 우항의 r(x)는 입력을 의미(ex: 힘, 전류, 변위 등)
* y(x)는 입력에 대한 출력

- y'의 계수가 f(x)일 때 f(x)를 나누어 아래와 같이 y'의 계수를 1로 만들었을때의 미방을 1계 선형 상미방의 표준형
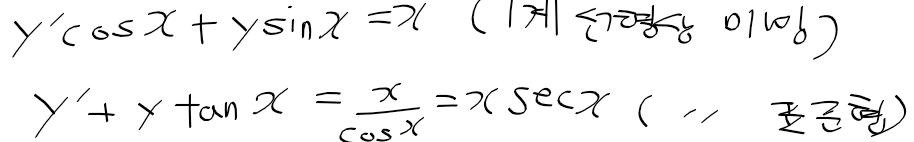
동차와 비동차
- 아래와 같이 우항이 0인 선형미분방정식을 동차 선형미방이라 하고, 0이 아닌 경우를 비동차 선형미방이라 한다.
- 동차 선형 미분 방정식 : 모든 항이 y 혹은 y의 도함수를 가지고 있다.
- 비동차 선형 미분 방정식 : 모든 항이 y 혹은 y의 도함수를 가지고 있지는 않다.
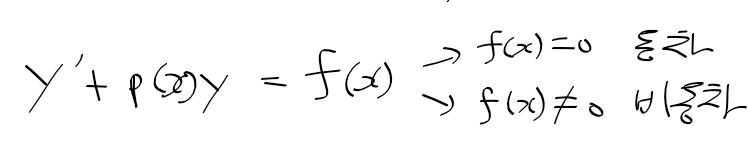
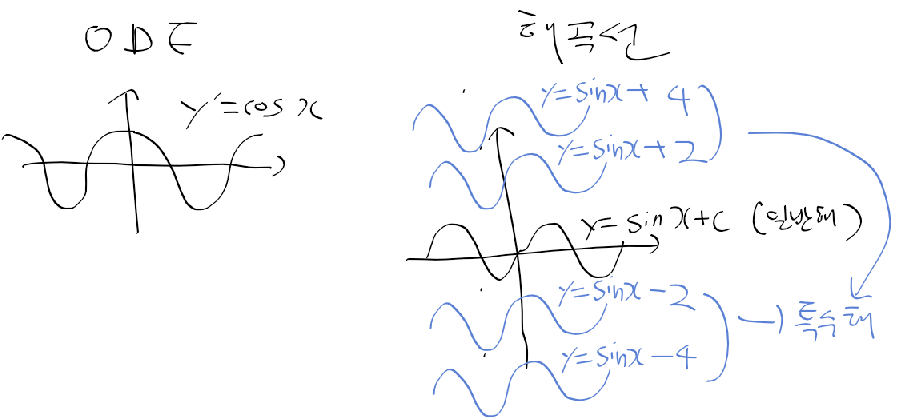
동차 선형 미방과 자명해(trivial solution)
- 다음의 동차 선형 미방의 표준형을 변수 분리하고, 적분 한후, 지수함수를 취하면 아래의 일반해(동차해)를 얻음
- 이 일반해에 c = 0을 대입하면 해당 구간 모든 x에 확실한 자명해 y(x)=0이나옴
* 자명해는 당연한 해로 필요 x
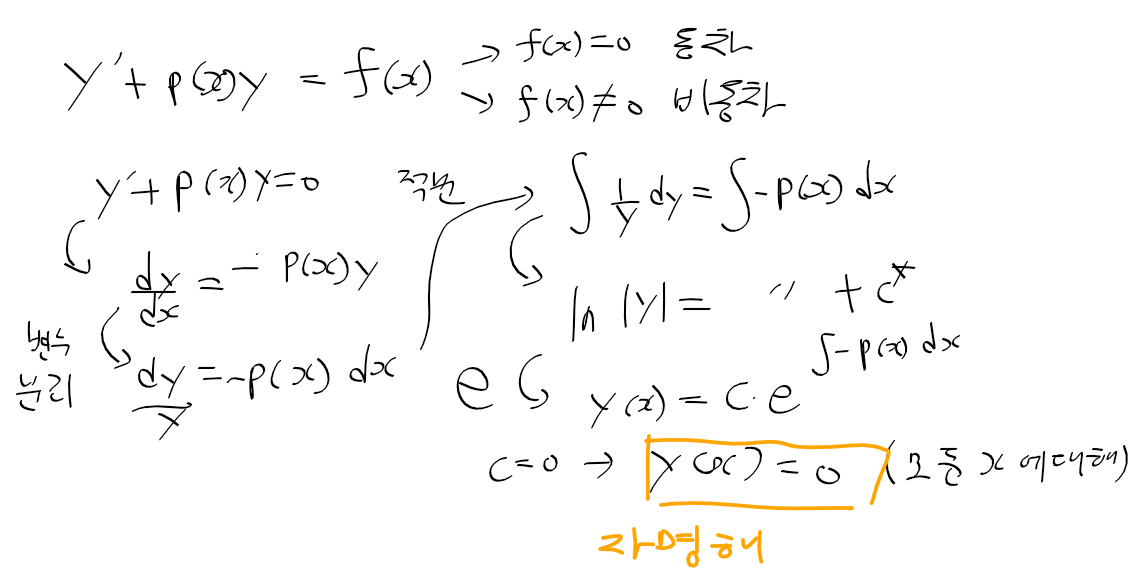
비동차 선형 미방의 해
- 아래의 비동차 선형 미방이 주어질때, 적분 인자 F를 곱하자
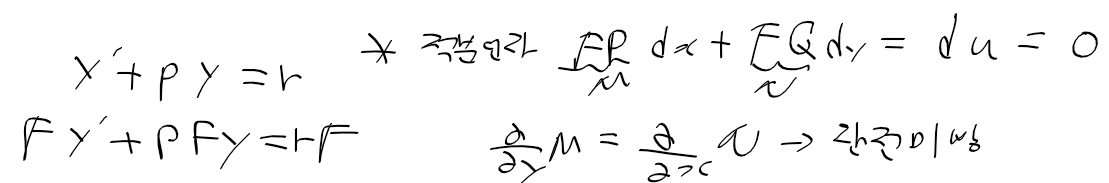
- pF = F'의 조건을 주고, 변수 분리법으로 분리한 후, 적분과 지수함수를 취한 결과 F = e^h가 나온다.
- 이를 Fy의 합성함수 미분 식에다가 대입한 결과. (Fy)' = r * F임을 얻는다.
- (Fy)'를 적분 후, 양변에 F(=e^h)를 나눈 결과 응답 y(x)에 대한 식이 나오며, 입력의 응답과 초기조건응답으로나뉜다.

ex1) 1계 선형 상미분방정식의 초기값이 주어질때 응답 y 구하기
- 아래의 미분방정식과 초기조건, y에 대한 식이 주어지면 입력 r = sin 2x, p = tanx
- h = p = tan x의 적분이며 e^h = sec x가 나온다. 이를 통해 식 y의 r*e^h와 e^-h를 구한다.
- 정리한 식 y에 초기조건을 대입한 결과 c = 3이 나왔으므로, 이 선형 미분 방정식의 특수해는 아래와 같다.
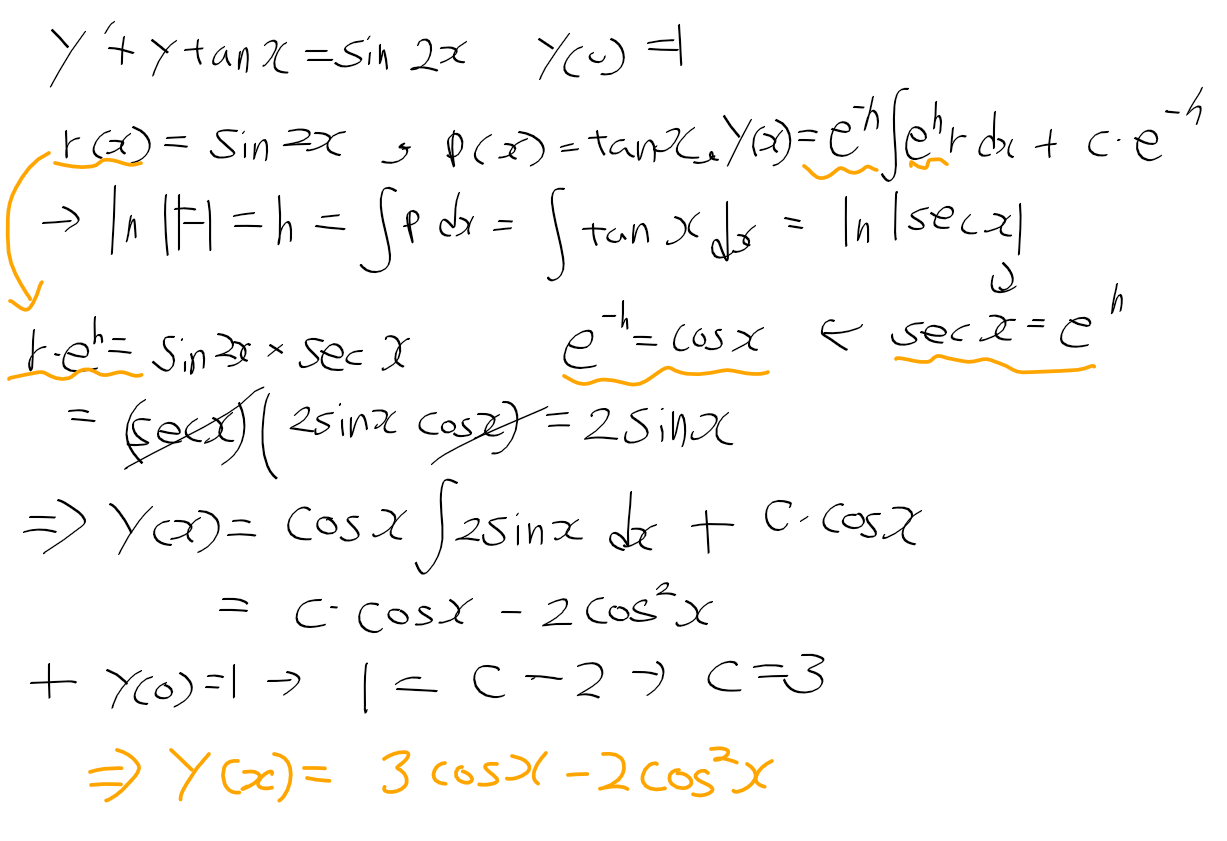
ex2) RL 회로의 전류를 구해보자
- RL 회로가 주어지면, KVL과 옴의법칙을 통해 구한 1계 선형 상미분방정식과 그의 표준형은 다음과 같다
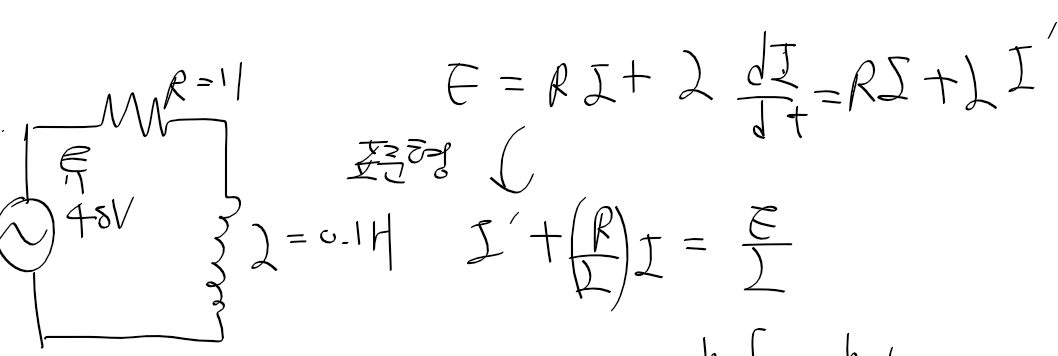
- 비동차 선형미방의 일반 해를 구해보자
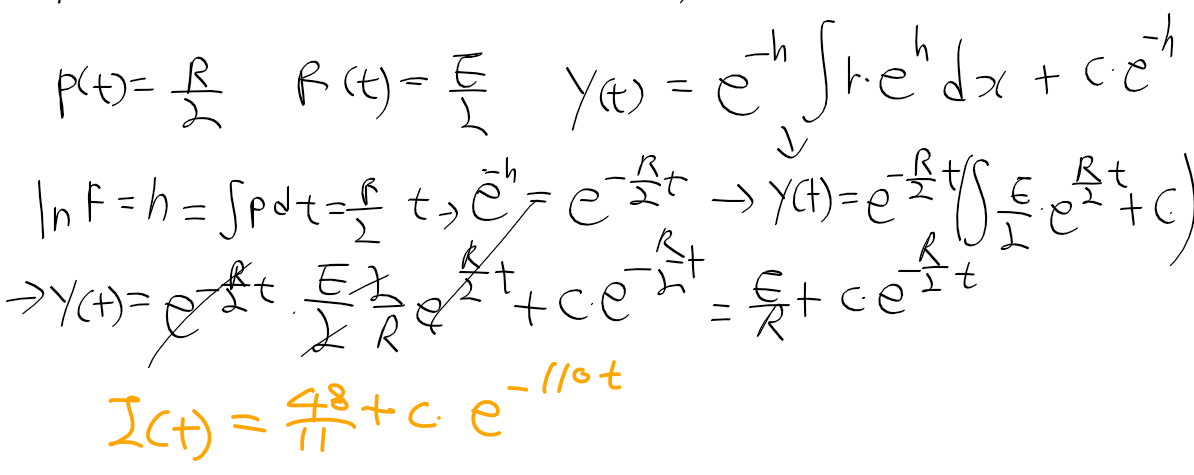
- 초기조건 I(0) = 0 <= 인가 시작떄 전류가 0이다. 초기조건을 통해 특수해를 구하자
* 회로이론의 RL회로 전류 인가시 전류의 과도응답 식과 같다! wow
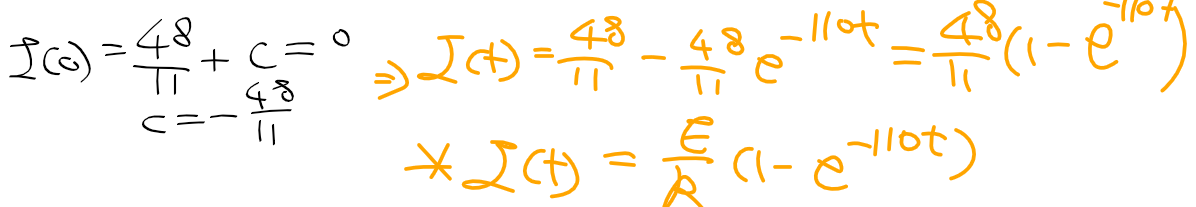
베르누이 방정식(비선형 상미방을 선형 상미방으로 바꾸기)
- 베르누이 방정식 : 실제 많은 문제는 비선형 -> 선형 상미분으로 변환하면 쉽게 풀수 있있으며 이 방법 중 하나
- 아래의 식에서 우항 y의 차수가 0 or 1이면 선형이지만 그렇지 않으면 비선형 상미방이 된다.
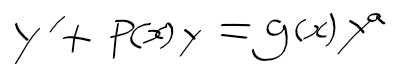
- 아래의 u에 대한 식을 미분하고 y'를 대입하자. u에 대한 선형 상미방이 나온다!
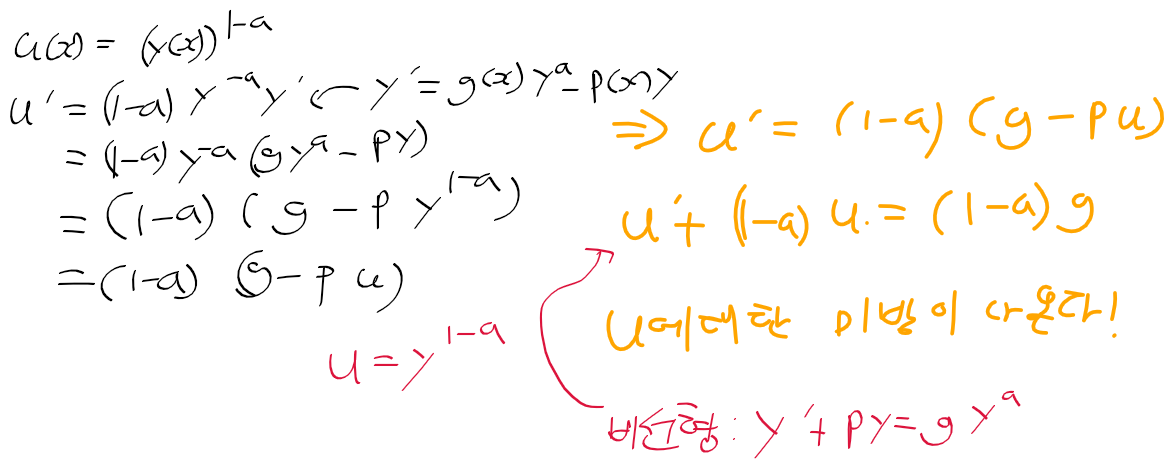
'수학 > 공업수학' 카테고리의 다른 글
| 공업수학 2 - 변수분리법과 완전미분방정식 (0) | 2022.05.11 |
|---|---|
| 공업수학 1 - 1계 상미분 방정식 기초와 오일러 방법을 이용한 근사치 구하기 (0) | 2022.05.10 |