공업수학 1 - 1계 상미분 방정식 기초와 오일러 방법을 이용한 근사치 구하기

미분 방정식 differential equation

- 현실의 물리 현상을 미분을 통해 모형화 한 방정식

- 상미분 방정식 ode ordinary de : 변수가 한개인 미방

- 편미분 방정식 pde partial de : 변수가 여러개인 미방

- 모델링 : 공학, 물리학, 화학 등 여러 분야의 실제 현상을 수학적으로 계산할 수 있도록 표현한 모델

 

 

* 목표 : 현실 문제에서상미분 방정식을 유도(모델링)하고, 방정식을 풀고 그래프 시각화하여 해석하자

 

1계 상미분 방정식

- 2차, 3차등 고차 도함수가 아닌 1차/1계 도함수만을 가지고 있는 미분방정식

 

 

공학 문제와 모델링

- 공학 문제를 계산을 통해 풀려면 수학 모델로 만들며 이를 모델링이라 함

- 모델링에 미방을 사용하는 이유 ? -> 다양한 물리 현상들이 도함수(미분)을 포함하고 있음(ex:속도, 가속도)

 

 

상미분방정식과 편미분 방정식

- 상미방 : 하나의 변수 <-> 편미방 : 여러 변수

 

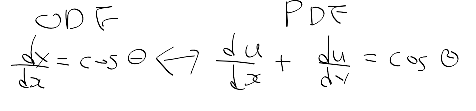
미분 방정식 활용 예시

- 낙하, 스프링에서 변위, RLC 회로 전류, 진자 운동

 

 

 

 

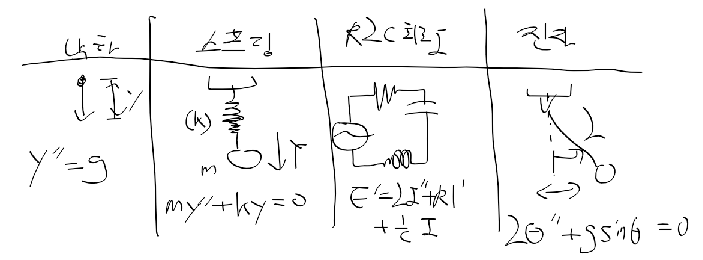
상미분방정식의 양형태, 음형태

- 양형태 explicit form : 모든 항을 좌변으로 옮김

- 음형태 implicit from : 도함수만 좌변으로 옮김

 

 

 

 

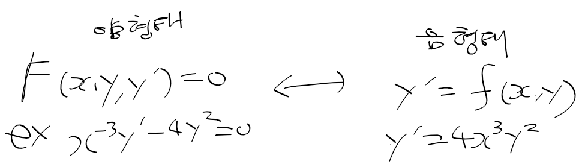
해

- 해 : 어느 함수 h(x)가 열린 구간에서 정의/미분 가능하며, 이 함수 h(x)를 만족하는 y

- 해곡선 : 해들의 곡선

- 열린 구간 : a < x < b에서 양 끝 a와 b를 포함하지 않는 구간

 

 

 

 

상미분 방정식과 해

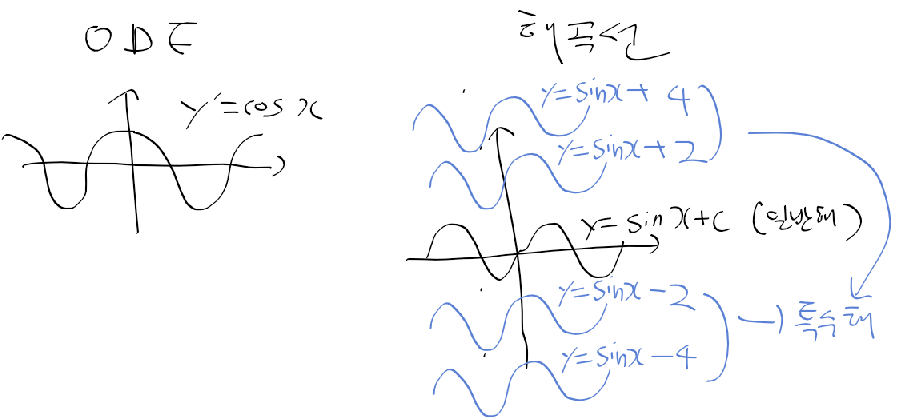
- y' = cos x인 (음형태) 상미분방정식이 있을때, ode의 해는 y = sin x + C

- 일반해 general solution : 임의의 상수 C를 가지고 있는 해

- 특수해 particular solution :  임의의 상수 C를 특정값으로 할때의 해

 

 

 

특수해와 초기값

- 초기조건 : 특정 입력값에 대한 출력 -> 일반해에 대입해 임의의 변수 c 값을 구할 수 있다.

 => 초기조건을 통해, 해당 초기조건의 특수해를 구한다.(초기값 문제)

 

 

 

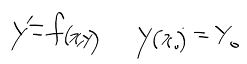
초기값 문제 예시

- y' = 3y, y(0) = 5.7일 때 특수해를 구해보자

 * y' = 3y : y를 미분했더니 y가 나온다 y는 지수함수의 형태다.

 * 구한 일반해에 위 초기조건을 대입하여 C를 구하

=> 특수해 y = 5.7 e^3x

 

 

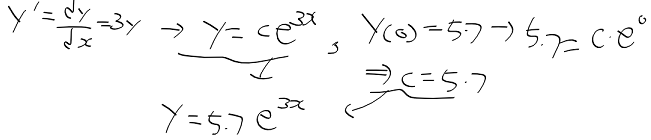
해석적 방법과 수치적 방법

- 해석적 방법 : 직접 계산하여 정확한 해를 구함

- 수치적 방법 : 근사화를 통해 해를 구함

 

1계 ode의 기하학적 의미

- y' = f(x, y)를 기하학적으로 해석해보자

- 점 (x0, y0)을 지나는 위 ode의 해곡선은 y'(x0) = f(x0, y0)을 만족해야한다.

 -> 그래픽 or 수치해석적 방법으로 ode의 근사해를 얻을 수 있다.

 

 

 

상미분 방정식의 방향장 시각화

- y' = y + x라는 상미분 방정식이 주어질 때, (0, 1), (0, 0), (0, -1) 세 점을 지난다면

 -> 3개의 해곡선을 가지며, 세 해곡선과 해당 ode의 방향장은 다음과 같다.

* 뒤에 오일러방법 계산하다가 자꾸 값이 이상하게 나왔는데 일반해부터 잘못 구한거같다

 

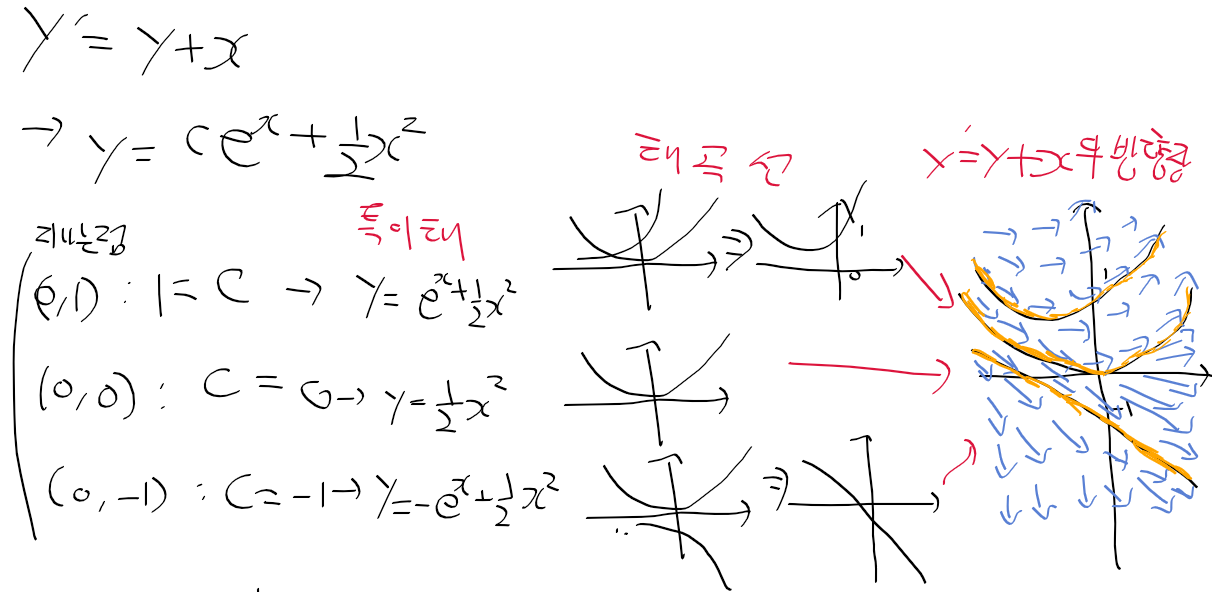
오일러 방법 - 간단한 수치해석적 방법

- ode와 초기값이 주어질 때, x1 = x0 + h라면

  => y1 = y0 + h * y' = y0 + h * f(x0, x0)

- 간격 h가 작을수록 오차는 줄어든다.

- h = 0.2로 놓고 구한 근사값과 실제 특이해를 비교하면 오차가 점점 커지는걸볼수있다.