이전 글에서는 대충 미분 방정식이 무엇이고
종류와 각 미방이 어떤 현실의 현상을 표현하고 있는지 간단하게 정리했다.
이번에는 실제 미방을 풀어내는 과정을 다뤄보려고 한다.
1. 일정 비율(mu)로 증가하는 종의 개체수 구하기
2. 구름 물방울이 떨어지는 속도 구하기
* 블로그에 latex 인가 뭐 스크립트 넣으면 그리스어 변환되기는 한데 넣기 귀찬아서 mu라 대충 적음
일정 비율(mu)로 증가하는 종의 개체수를 미방으로 풀어보기(변수분리법 사용하기)
- 대충 토끼의 경우 많으나 적으나 일정 비율로 증가한다고 가정하자
- 토끼가 적으면 적지만 (적은 개체수 x mu)만큼 증가하고 많은데로 (많은 개채수 x mu) 증가한다. 이를 미방을 표현하면 다음과 같다
* 여기서 말하는 일정 비율 mu는 현실의 데이터로 가장 적당한 값을 구해서 쓰면된다. 적당한게 없으니 그냥 변수로 놓자
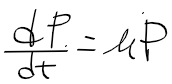
- 이 미방으로부터 해 P 그러니까 P(t)를 구하기 위해 우선 우항의 P를 좌항으로 보내주자.
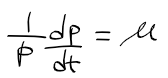
- 좌측 항에 dp와 dt가 붙어있다. 이 변수들을 이렇게 분리시켜보자(변수분리법)
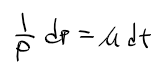
- 여기서 부정적분을 한 후 계산하면 다음과 같이 정리된다.

- ln P = ut + C이므로 이를 P에 대한 식으로 고쳐주면, 미분방정식의 해 P(=P(t))가 나온다.
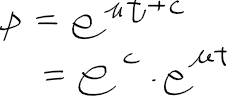
- 여기에 e^c를 대충 처음 인구수(초기조건) P0라 한다면 다음과 같이 정리된다
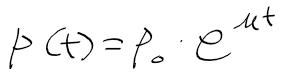
- mu가 0보다 크면 mu만큼 지수적으로 증가할것이고, mu가 0보다 작으면 인구는 줄어들것
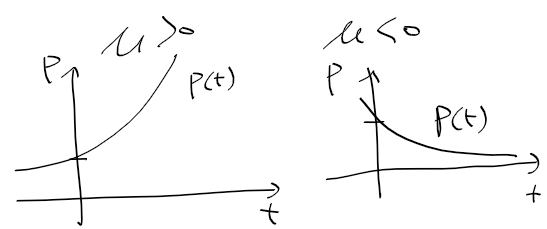
mu비율 만큼 증가하는 개체수 모델의 문제
- 방금 모델링한 미방의 해를 보면 지수적으로 증가하나 실제 종은 지수적으로 증가하다가 한계에 도달하므로 현실을 완벽히 반영못함
=> 현실을 잘 반영하는 미방 모델을 설계해야한다.
미정 계수법
- 비동차 미분방정식의 해를 구하는 방법으로 미정-정해지지않은 계수를 구하는 방법
- 대충 비동차 미분방정식, 우항이 0이 아닌 미방을 푸는데 사용된다 정도만 이해하고 넘어가자
떨어지는 물체의 속도와 빗방울이 만나는 저항
- 중력을 몰랐을 시절 아리스토텔레스는 무거운 물체일수록 빠른 속도로 떨어진다고 생각하였으나, 진공을 가정 시(저항이 존재하지 않는다면) 모두 떨어지는 속도가 같음
- 빗방울 저항 : 하늘에서 떨어지는 빗방울에는 점성(끈끈이) 저항과 관성 저항(공기와 부딪혀 생김)이 반영
* 적당한 그림 찾아보려 했는데 안보인다 ㅜㅜ
하늘에서 떨어지는 물체의 속도를 구하는 미분 방정식을 구해보자
- 속도는 아래 방향을 향하고, 물체에 작용하는 중력도 아래 <-> 저항력은 반대를 향한다. 그림으로 하면 다음과 같다.
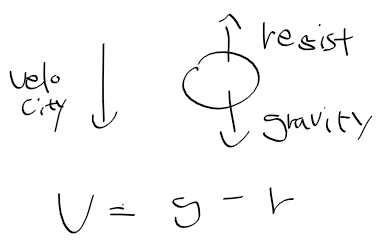
- 위에서 속도 v = 중력 g - 저항 r 이라 적긴 했는데 대충 적은 것일 뿐이고 ma = F로 제대로 표현해야한다.
- 여기서 외력 F는 중력 - 저항이긴 한데 저항은 점성 저항, 관성 저항으로 나누어서 표현하면 다음과 같다.
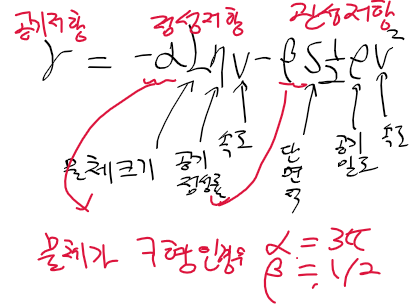
- 물체의 크기 L은 지름 2r, 단면적 S는 구의 면적 pi r^2이라 한다면 공기 저항은 다음과 같이 정리할 수 있다.
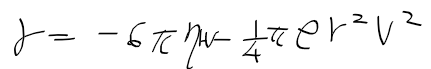
- 빗방울에 작용하는 힘 F = 중력 - 저항이므로 다음과 같이 정리할 수 있음
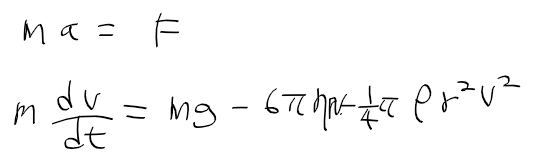
- 이걸 그대로 계산하기는 너무 복잡하므로 다음 두 경우로 나누어서 생각해보자
1) 구름 물방울 : 아주 작으므로 점성 저항만 작용된다
2) 빗방울 : 무거워 빨리 떨어지므로 관성 저항만 작용된다.
* 작을수록 점성저항, 클수록 관성 저항의 영향이 크다.
(비동차 미방 풀기) 구름 물방울이 떨어지는 속도 구하기
1) 우항이 0이일때의 해 일반해를 구한다
2) 일반해와 초기조건을 이용하여 특수해를 구한다
- 구름 물방울은 빗방울에 작으므로 미방을 다음과 같이 정리하자
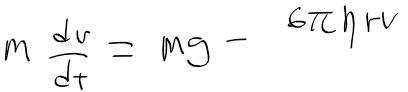
- 좌우항을 질량 m으로 나눈 후, 우항 v의 계수 6 * pi * r /m이 너무 복잡하므로 A로 놓으면 다음과 같이 정리됨.
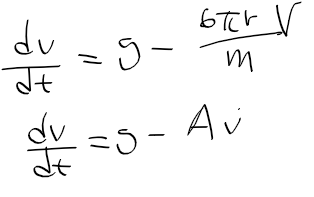
- v가 붙어있지 않은 g를 제외하고 모두 우항으로 보내면 비동차 미분방정식임을 알수 있다.
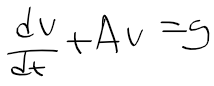
- 비동차 미분방정식을 풀기위해 g를 0으로 놓고 일반해부터 구하자
(마지막 e^c는 그냥 c로 놓자)
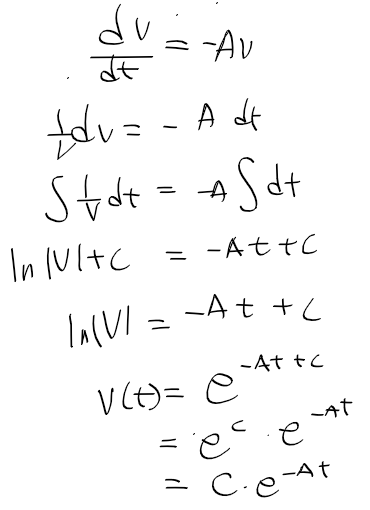
- 기존 미방에 다시 돌아와 v(t) = c * e^(-At)에서 c = c(t)로 놓고, 일반해 v(t) = c(t) * e^(-At)를 대입해서 풀어보자
- 좌항을 두 함수 곱의 미분 정리로 풀면 아래와 같이 정리된다.
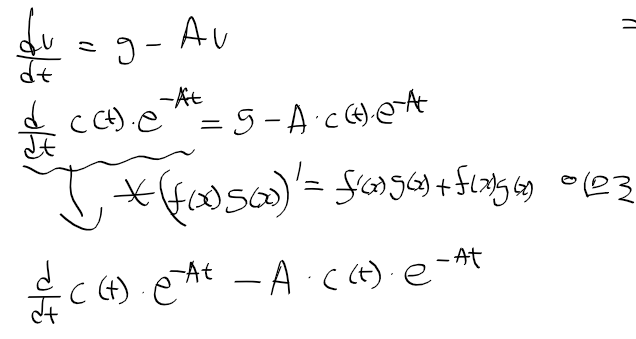
- 대입한 후 정리하면 c(t)에 대한 식이 만들어 진다.
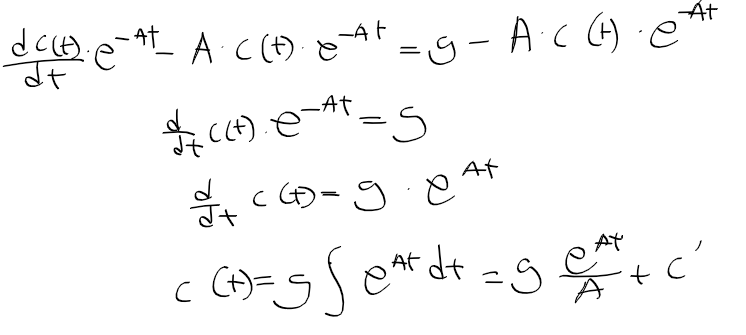
- 구한 c(t)를 원래 일반해 v(t) = c(t) * e^(-At)에다 대입하면, 시간 흐름에 대한 속도 변화 v(t)가 나온다.
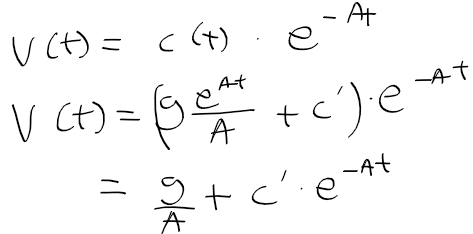
- 초기속도 v(0) = 0으로 하여 c'를 구한뒤 다시 v(t)를 정리하면 다음과 같음
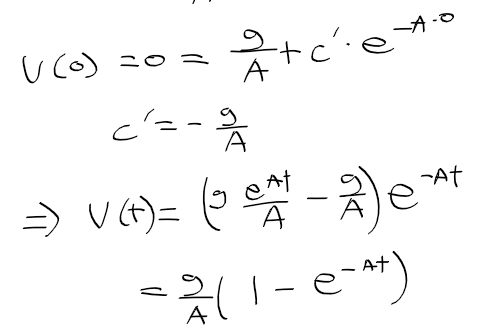
- 결국에 v(t)는 어떤 그래프 모양이 될까? 아무것도 정해진게 없으니 구할수는 없지만 지수함수 e^x와 e^-x의 형태를 생각해보자
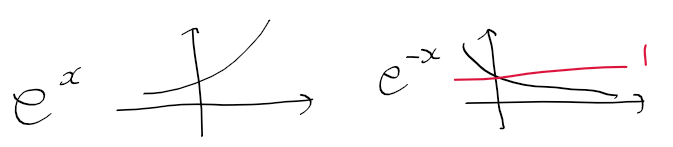
- 1-e^-x는 결국 0에서 시작해서 처음엔 빠르게 오르다 1에 가까워질 것이다
(e^-x 는 0에 수렴하므로)
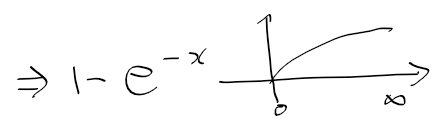
- 여기서 시간이 무한히 흐를때 최종적으로 가까워지는 속도를 종단 속도라 한다.
- t = 무한대로 놓고, 계속 나두던 A도 정리해보자
=> 결국 종단 속도는 mg(=중량)에 따라 정해진다!
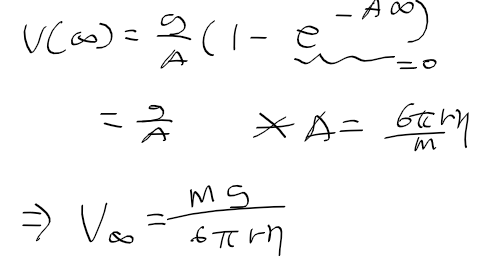
'요약' 카테고리의 다른 글
| 미분방정식으로 현실을 어떻게 수학 모델로 만들까 1 - 간단미방종류 (0) | 2023.09.20 |
|---|---|
| 컴퓨터 과학 관련 용어 1. 인코딩, 데이터 규격, 프로세서 관련 (0) | 2022.05.30 |
| 네트워크 간단 요약 (0) | 2022.05.29 |
| 로봇 공학 요약 - 로봇 종류부터 구성 요소, 구동기, 센서까지 (0) | 2022.05.05 |