센서 퓨전 진짜 오랜만에 보는데
일단 먼저 자이로 각속도로 오일러 각 구하기 구현 시작
1. 자이로로 부터 얻은 각속도로 오일러 각 구하기
일단 자이로 각속도 데이터부터 읽어오기 구현
제너레이터로 루프마다 가져오게 만듬
각속도 wx, wy, wz
import scipy.io
gyro = scipy.io.loadmat("ArsGyro.mat")
def get_gyro():
wx = gyro["wx"]
wy = gyro["wy"]
wz = gyro["wz"]
gyro_len = len(wx)
for i in range(gyro_len):
yield wx[i], wy[i], wz[i]
for wx, wy, wz in get_gyro():
print(wx, wy, wz)
get_gyro()
xyz니까 한번 플로팅해주려고 하는데 할때마다 서브플롯 어캐햇는지 잊어먹는다

import matplotlib.pyplot as plt
plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax2 = plt.subplot(3,1,3)
대충 이거랑 get gyro랑 섞으면 이래 나온다.
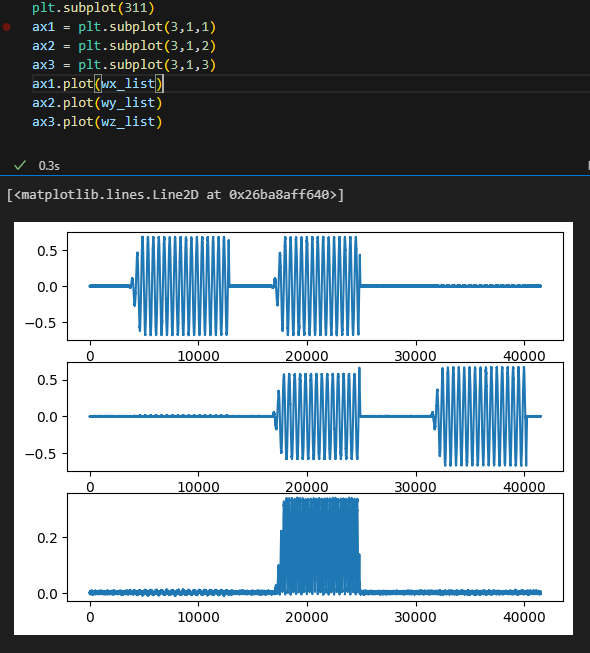
wx_list = []
wy_list = []
wz_list = []
for wx, wy, wz in get_gyro():
wx_list.append(wx)
wy_list.append(wy)
wz_list.append(wz)
plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(wx_list)
ax2.plot(wy_list)
ax3.plot(wz_list)
2. 각속도 -> 오일러각 변환하기
이번에는 각속도 wx,wy,wz를 pqr이라 하자
이걸 오일러각 phi theta psi 로 바꾸도록 구현
얻어내고자 하는 오일러각(변화량)은
기존의 오일러 각으로 아래 3 x 3 행렬 구하고 p q r 과 곱하면 나옴
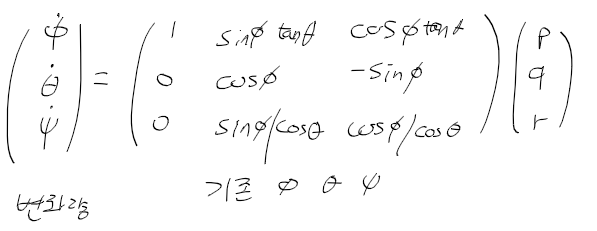
매트랩 코드를 파이썬으로 구현하는데
이전 파이 세타 프사이를 매개변수로 넣어버릴까 싶다가
그냥 메트랩 코드 따라서 전역으로 나둠
일단 대충 구현하면 이런식이다
from math import cos, sin, tan
prev_phi = 0
prev_theta = 0
prev_psi = 0
def gyro_euler(p, q, r, dt):
sin_phi = sin(prev_phi)
cos_phi = cos(prev_phi)
cos_theta = cos(prev_theta)
tan_theta = tan(prev_theta)
phi = prev_phi + dt * (p + q * sin_phi * tan_theta + r * cos_phi * tan_theta)
theta = prev_theta + dt * (q * cos_phi - r * sin_phi)
psi = prev_psi + dt * (q * sin_phi / cos_theta + r * cos_phi / cos_theta)
return phi, theta, psi
각속도 -> 오일러 변환 모듈을 플로팅함수랑 합치자
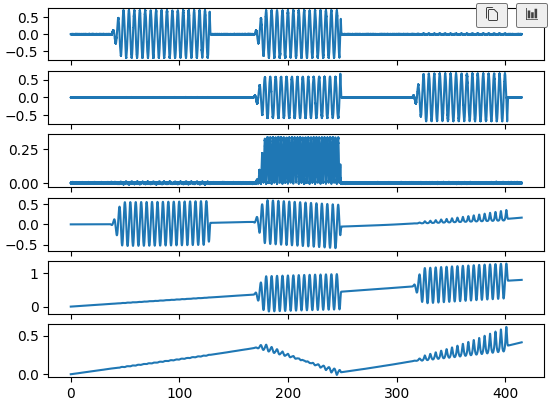
위 그래프 3개는 각속도
아래 3개는 오일러각
z축 회전은 그렇다 쳐도
x, y를 보면 오차가 누적되서 롤 피치각이 기울어진 모양을 하고있음
3. 가속도계 값 가져오기
자이로는 됫으니 가속도계 가져올 차례
자이로랑 별차이 없다 이름만 조금 고쳐줌
import scipy.io
accel = scipy.io.loadmat("ArsAccel.mat")
def get_accel():
ax = accel["fx"]
ay = accel["fy"]
az = accel["fz"]
accel_len = len(ax)
for i in range(accel_len):
yield ax[i], ay[i], az[i]
for ax, ay, az in get_accel():
print(ax, ay, az)
get_accel()
이것도 플로팅해보면
잘 나온다.

ax_list = []
ay_list = []
az_list = []
for ax, ay, az in get_accel():
ax_list.append(ax)
ay_list.append(ay)
az_list.append(az)
plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(ax_list)
ax2.plot(ay_list)
ax3.plot(az_list)
4. 회전하지 않고, 등속도 운동 상황 가정시 자세 구하기
이제 가속도를 쓰려고 하는데 좀 복잡하게 생김
가속도에는 회전 영향도 있고, 중력 영향도 있음
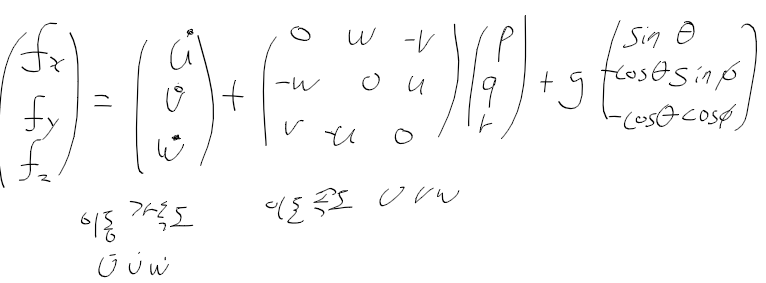
등속운동 중이고, 회전을 안한다 가정시, 위 식을 단순하게 만들어서
fx, fy, fz를 가지고 파이와 세타를 구할 수 있음
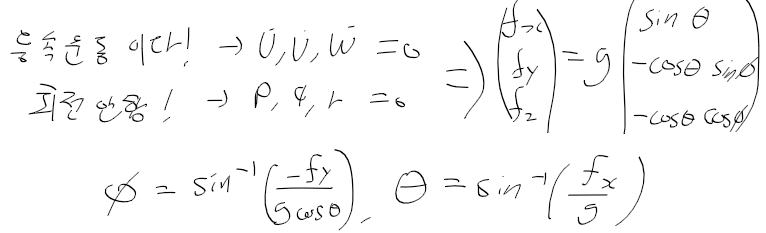
xyz 가속도로 파이 세타 가져오는 함수 구현하면 이럼
from math import asin, acos
def accel_euler(ax, ay, az):
g = 9.8
theta = asin( ax / g)
phi = asin(-ay / (g * cos(theta)))
return phi, theta
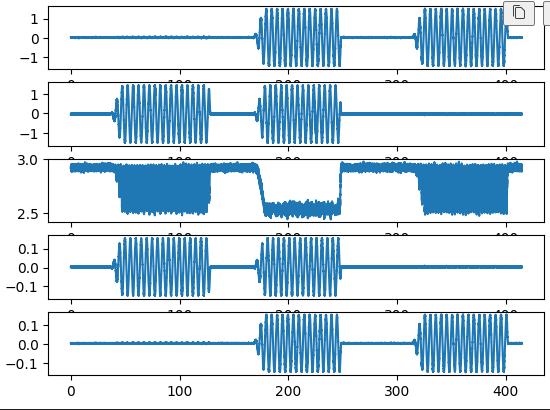
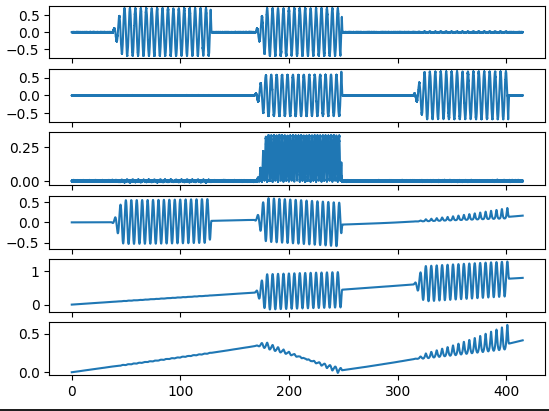
이것도 그래프 플로팅 시키면
파이, 세타
롤피치요 니까
아래 2개는 롤각과 피치각을 나타냄
import numpy as np
def accel_euler(ax, ay, az):
g = 9.8
theta = asin( ax / g)
phi = asin(-ay / (g * cos(theta)))
return phi, theta
dt = 0.01
t_list = np.linspace(0, 415, 41500)
ax_list, ay_list, az_list = [], [], []
phi_list, theta_list = [], []
for ax, ay, az in get_accel():
phi, theta = accel_euler(ax, ay, az)
ax_list.append(ax)
ay_list.append(ay)
az_list.append(az)
phi_list.append(phi)
theta_list.append(theta)
plt.subplot(511)
ax1 = plt.subplot(5,1,1)
ax2 = plt.subplot(5,1,2)
ax3 = plt.subplot(5,1,3)
ax1.plot(t_list, ax_list)
ax2.plot(t_list, ay_list)
ax3.plot(t_list, az_list)
ax4 = plt.subplot(5,1,4)
ax5 = plt.subplot(5,1,5)
ax4.plot(t_list, phi_list)
ax5.plot(t_list, theta_list)
5. 센서 퓨전을 통한 자세 구하기
앞서 자이로만 가지고 파이 세타 프사이 자세를
가속도계만 가지고 파이 세타 자세를 계산해봄
이번에는 kf로 자이로와 가속도 데이터 센서 퓨전함
자이로, 가속도 계 데이터 보면
자이로로 구한 자세는 오차가 누적
가속도계로 구한 자세는 오차 누적되진 않음
=> 자이로 데이터로 자세를 먼저 구하고, 누적되는 오차는 가속도 계로 보정
! 오일러각 대신 쿼터니언 사용
X를 파이 세타 프사이로 놓으면 시스템 행렬 A를 만들수가 없다
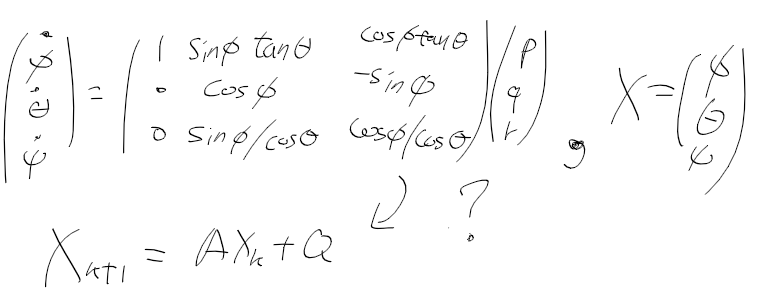
대신 쿼터니언을 사용하면 각속도 pqr과 쿼터니언을 이런식으로 정리 가능
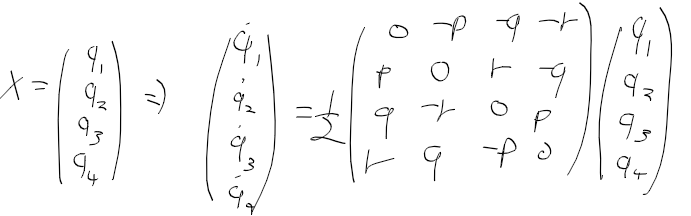
k+1, k 이산 시간에 대해 수정하면 이런식으로 정리해서 A를 구할수 있음
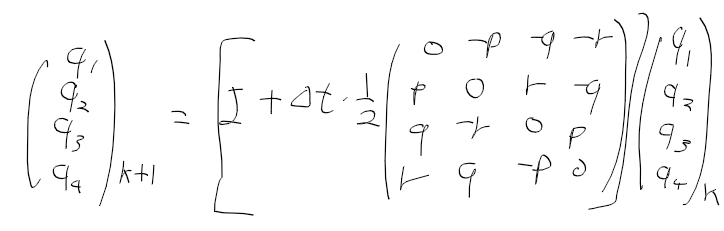
쿼터니언과 오일러각 사이 관계는 이런식이라고 함
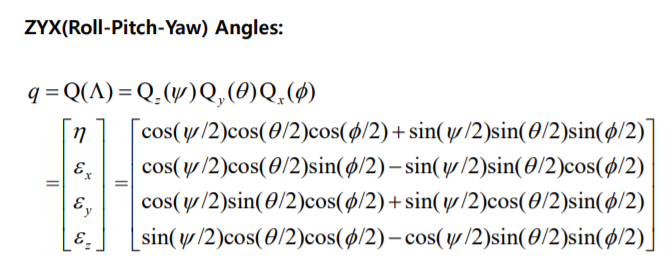
지금까지 구현한 kf에서는
시스템 행렬 A가 고정 되어있었는데
지금 시스템 행렬 A는 각속도 pqr에 따라 계속 변해서 이전 구현 내용과는 살짝 다름
이전 kf에서는 z만 넣어줬찌만
이번 kf에는 A, z를 같이 넣는다
잠깐 구현 중에 다시 정리한다
1. 각속도 -> 시스템 행렬 A 만듬
2. 가속도계 -> 오일러각 변환 phi, theta 취득 -> 쿼터니언으로 변환하여 z로 사용
미완 코드
def kf_euler(A, z):
X_pred = A @ X
P_pred = A @ P @ A.T + Q
K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
X_est = X_pred + K @ (z - H @ X_pred)
P_est = P_pred - K @ H @ P_pred
return X_est, P_est
dt = 0.01
X = np.array([[1, 0, 0, 0]]).T
H = np.array([
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
Q = 0.0001 * np.eye(4)
R = 10 * np.eye(4)
P = np.eye(4)
for (p, q, r), (ax, ay, az) in zip(get_gyro(), get_accel()):
A = np.array([
[0, -p, -q, -r],
[p, 0, r, -q],
[q, -r, 0, p],
[r, q, -p, 0]
])
A = np.eye(4) + dt * 1/2 * A
phi, theta = accel_euler(ax, ay, az)
내가 여기서 빠트린게 오일러각으로 쿼터니언 변환을 구현안했다
아까 그림대로 만들면 되는데 되게 복잡하네
구현하다보니 kf 결과는 쿼터니언으로 반환하니
알아보게 시각화하려면 쿼터니언을 오일러각으로 다시 바꿔줘야 한다..
이건 엄두가 안나는데 메트랩코드 그대로 파이썬으로 고쳐줌
def quaternion_to_euler(X):
x1 = X[0][0]
x2 = X[1][0]
x3 = X[2][0]
x4 = X[3][0]
phi = atan2( 2*(x3*x4 + x1*x2), 1 - 2*(x2**2 + x3**2) )
theta = -asin( 2*(x2*x4 - x1*x3))
psi = atan2( 2*(x2*x3 + x1*x4), 1 - 2*(x3**2 + x4**2))
return phi, theta, psi
아 하다가 겟 자이로, 가속도에서 좀 잘못구현한거같은데
wx[i] 이던걸 뒤에 [0] 인덱싱 추가해줘야 kf 계산에서 잘못안댐
import scipy.io
gyro = scipy.io.loadmat("ArsGyro.mat")
def get_gyro():
wx = gyro["wx"]
wy = gyro["wy"]
wz = gyro["wz"]
gyro_len = len(wx)
for i in range(gyro_len):
yield wx[i][0], wy[i][0], wz[i][0]
for wx, wy, wz in get_gyro():
print(wx, wy, wz)
get_gyro()
import scipy.io
accel = scipy.io.loadmat("ArsAccel.mat")
def get_accel():
ax = accel["fx"]
ay = accel["fy"]
az = accel["fz"]
accel_len = len(ax)
for i in range(accel_len):
yield ax[i][0], ay[i][0], az[i][0]
for ax, ay, az in get_accel():
print(ax, ay, az)
get_accel()
자이로, 가속도계를 이용해서 노이즈를 제거한채 자세 추정이 잘 되었다
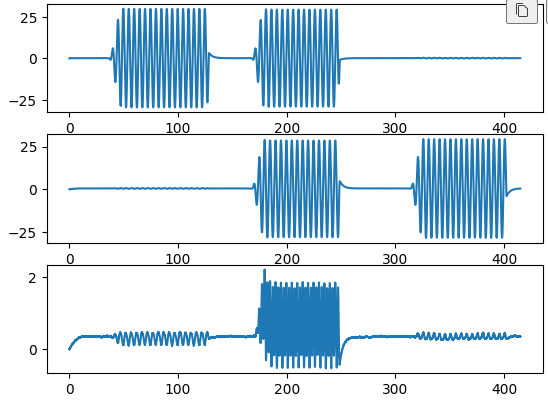
아래 그림은 아까 자이로 각속도에서 오일러각 계산한 그래프인데
4, 5번째 파이 세타가 오차 누적되서 기울어졌었지만 지금은 가속도 계 덕분에 누적 오차를 제거해서 윗 그림처럼 원하는 결과 얻어내었다.
from math import atan2
from math import pi
def euler_to_quaternion(phi, theta, psi):
sin_phi = sin(phi / 2)
cos_phi = cos(phi / 2)
sin_theta = sin(theta / 2)
cos_theta = cos(theta / 2)
sin_psi = sin(psi / 2)
cos_psi = cos(psi / 2)
z = np.array([
[
cos_phi * cos_theta * cos_psi + sin_phi * sin_theta * sin_psi,
sin_phi * cos_theta * cos_psi - cos_phi * sin_theta * sin_psi,
cos_phi * sin_theta * cos_psi + sin_phi * cos_theta * sin_psi,
cos_phi * cos_theta * sin_psi - sin_phi * sin_theta * cos_psi
]
]).T
return z
def quaternion_to_euler(X):
x1 = X[0][0]
x2 = X[1][0]
x3 = X[2][0]
x4 = X[3][0]
phi = atan2( 2*(x3*x4 + x1*x2), 1 - 2*(x2**2 + x3**2) )
theta = -asin( 2*(x2*x4 - x1*x3))
psi = atan2( 2*(x2*x3 + x1*x4), 1 - 2*(x3**2 + x4**2))
return phi, theta, psi
def kf_euler(A, z):
X_pred = A @ X
P_pred = A @ P @ A.T + Q
K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
X_est = X_pred + K @ (z - H @ X_pred)
P_est = P_pred - K @ H @ P_pred
return X_est, P_est
dt = 0.01
t_list = np.linspace(0, 415, 41500)
phi_list, theta_list, psi_list = [], [], []
X = np.array([[1, 0, 0, 0]]).T
H = np.array([
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
Q = 0.0001 * np.eye(4)
R = 10 * np.eye(4)
P = np.eye(4)
for (p, q, r), (ax, ay, az) in zip(get_gyro(), get_accel()):
A = np.array([
[0, -p, -q, -r],
[p, 0, r, -q],
[q, -r, 0, p],
[r, q, -p, 0]
])
A = np.eye(4) + dt * 1/2 * A
phi, theta = accel_euler(ax, ay, az)
z = euler_to_quaternion(phi, theta, 0)
X, P = kf_euler(A, z)
phi, theta, psi = quaternion_to_euler(X)
phi_list.append(phi * 180 / pi)
theta_list.append(theta * 180 / pi)
psi_list.append(psi * 180 / pi)
plt.subplot(311)
ax1 = plt.subplot(3,1,1)
ax2 = plt.subplot(3,1,2)
ax3 = plt.subplot(3,1,3)
ax1.plot(t_list, phi_list)
ax2.plot(t_list, theta_list)
ax3.plot(t_list, psi_list)
'컴퓨터과학 > 필터' 카테고리의 다른 글
| 칼만필터 파이썬 - 9. 무향 칼만 필터 (0) | 2023.10.04 |
|---|---|
| 칼만필터 파이썬 - 8. 확장 칼만 필터 (0) | 2023.10.04 |
| 칼만필터 파이썬 - 6. 칼만 필터를 이용한 추적기 구현 (0) | 2023.10.03 |
| 칼만필터 파이썬 - 5. 칼만 필터를 이용한 위치로 속도 계산 (0) | 2023.10.02 |
| 칼만필터 파이썬 - 4. 단순 칼만 필터 구현 (0) | 2023.10.02 |