한 점을 지나는 접선의 방정식
- x0에서 연속인 함수 f(x)의 접선인 (기울기 a) 방정식은 다음과 같음
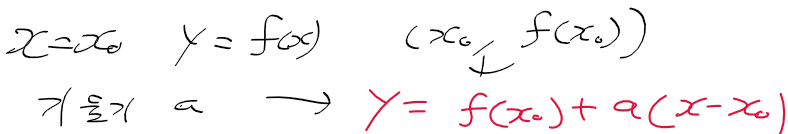
두 점을 지나는 직선의 기울기
- y = f(x)의 두 점 x0, x1을 지나는 직선의 기울기는 다음과 같다
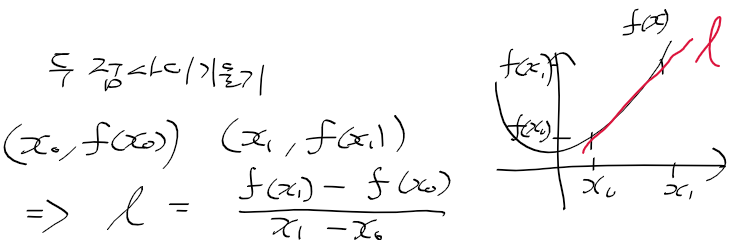
극한을 통한 접선의 기울기
- 위에서는 두 점을 지나는 직선의 기울기를 구함
- x1이 x0에 점점 가까워지면 x0에서의 점선에 대한 기울기가 나온다.

램프 함수의 기울기는?
- 자주 사용하는 램프 함수는 x가 0미만에서는 0이고, 0이상에서는 x이다. 그러면 램프 함수의 기울기는 어떨까
=> 램프 함수는 0에서 좌극한과 우극한이 다르므로 미분가능하지 않음

도함수
- 함수 f(x)의 한 점에서 기울기를 구하는 식 f'(x)
- x = x1인 지점에서 f(x)가 미분가능한 경우 도함수 f'(x)는 다음과 같음
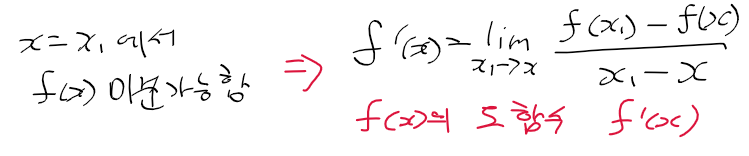
미분 계수와 도함수 차이
- 도함수 : 임의의 점 x에서 함수 y = f(x)의 접선 기울기를 구하는 식(x 미정)
- 미분 계수 : 특정한 x 지점에서의 기울기(x 지정)

미분 계수 표현하기
- 미분 계수 a는 dy/dx로 표현
- 미분 계수는 한 점에서의 기울기이므로 해당 지점은 다음과 같이 표현
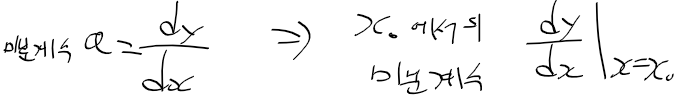
일차 근사
- 근사식 : 주어진 함수 y = f(x)에 가깝게 근사/표현한 식
- 일차 근사 : 일차 함수(= 직선에 대한 함수)로 y = f(x)에 가깞게 나타낸 식
- 실제 값과 근사 값의 차이 : x1에서 실제 함수와 (x0에서 선형 근사한)일차 근사 함수에는 다음과 같이 차이가 존재
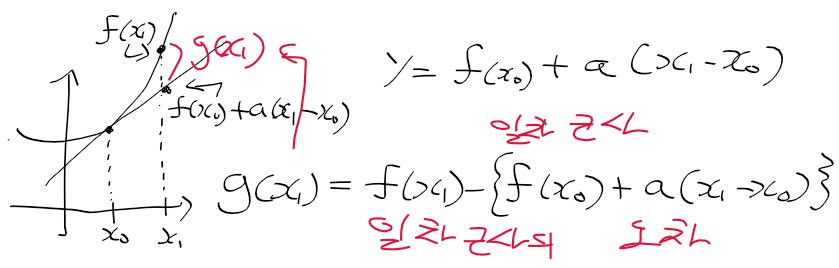
도함수와 미분의 의미와 도함수 예시
- 도함수 : 임의의 x에 대한 함수 y = f(x)의 접선 기울기를 구하는 식
- 미분 : f(x)의 도함수를 얻는 것
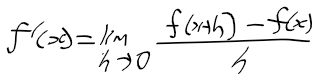
- 함수 f(x) = x, f(x) = x^2, f(x) = x^3 의 도함수 예시
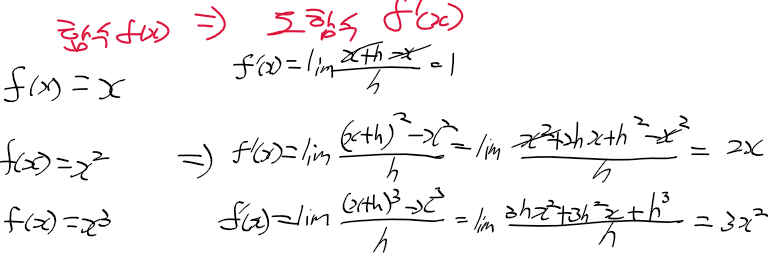
정적분과 구분구적법
- 정적분 : 함수의 면적을 구하는 방법
- 구분구적법 : 폐구간 I = [a, b]의 연속함수 f(x)의 각 작은 구간에 대한 직사각형을 합하여 면적 근사 계산한 방법

원시함수와 부정적분
- 부정적분 : 임의의 적분 가능한 구간에서의 정적분
- 원시함수 : F'(x) = f(x)를 만족하는 함수 F(x)
- 부정적분과 원시 함수의 관계 : 원시함수 = 부정적분 + 임의의 상수 C

'수학 > 해석,기하' 카테고리의 다른 글
| 기초해석학 - 6. 테일러 근사와 해석 함수 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 5.무한소와 테일러 공식 (0) | 2023.09.21 |
| 기초해석학 - 4. 초등함수 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |