테일러 급수를 이용한 근사
- 다항식 차수가 높아 질수록 더 넓은 범위로 근사값이 가까워 진다!
=> 테일러 급수는 연속미분가능함수를 n차 다항식으로 만들어 줄수 있음
=> n -> inf가 될때 얼마나 f(x)와 일치할까? 함수열의 수렴을 보아야함
- ln(1 + x)를 테일러 급수로 근사화한 모습
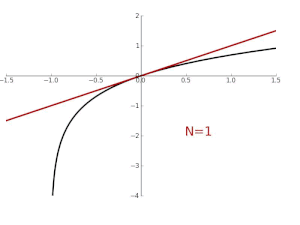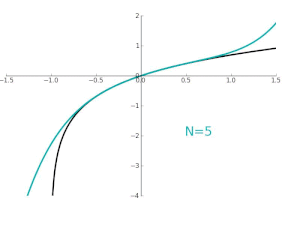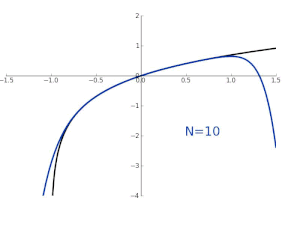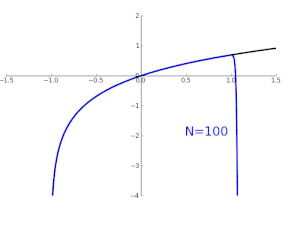
- 지수함수 y = e^x를 테일러 급수로 근사한 모습
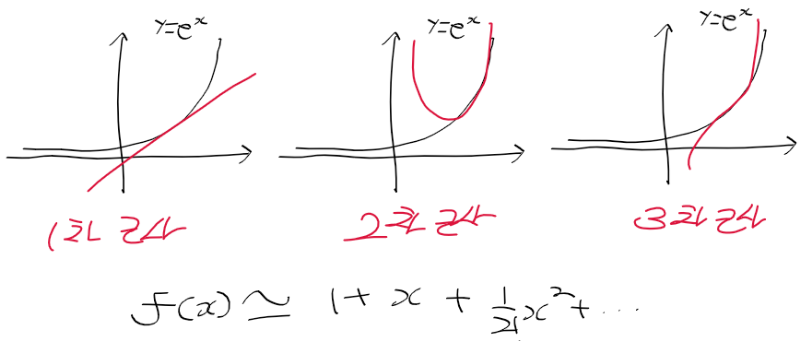
점멸수렴과 균등 수렴
- 점멸 수렴 : 구간 I의 함수열 fn(x)들이, 구간 I의 점 x0에 f(x)로 수렴하는 경우.
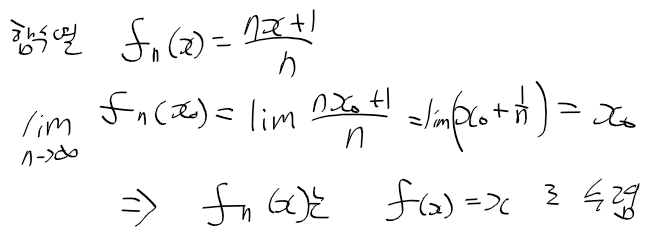
- 균등 수렴 : 함수열 fn(x) - f(x)의 차이 상한이 0으로 수렴하는 경우
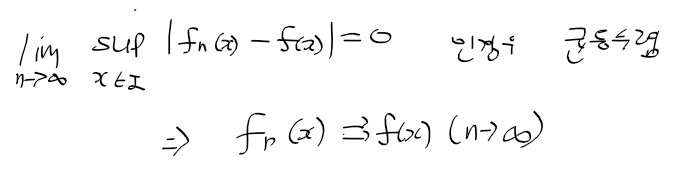
무한급수와 함수항 급수, 정급수
- 함수열 급수 : 함수열로 구성된 함수열
ex) 함수열 u_n(x)로 f_n(x)를 정의한 경우
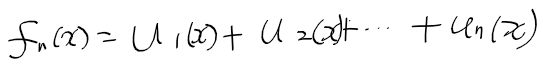
- 무한 급수와 함수항 급수 차이 : 무한 급수의 각 값이 값 대신 함수인 경우
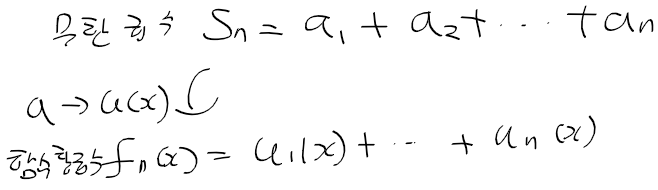
- 정 급수 : 다음의 모습을 띄는 함수항 급수, x0은 정급수의 중심

해석함수, 테일러 전개, 메클로린 전개
- 수렴 반경 :정급수 f(x)가 x0로부터 수렴할수있게 하는 범위
- 해석 함수 : 수렴 반경 r > 0인 정급수 f(x)가 임의의 점 x0에 대해 표현할 수 있는 경우 f(x)는 해석함수
(= 테일러 전개)
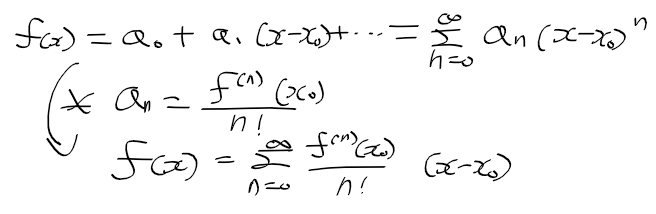
- 메클로린 전개 : 테일러 전개에서 x0 = 0인 경우
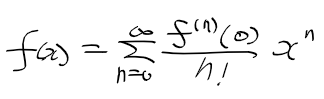
'수학 > 해석,기하' 카테고리의 다른 글
| 기초해석학 - 5.무한소와 테일러 공식 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 4. 초등함수 (0) | 2023.09.19 |
| 기초해석학 - 3. 미적분 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |