초등함수
- 다항함수, 지수함수, 로그함수 및 함수의 합성과 사칙연산으로 구할 수 있는 모든 함수
- (주의) 초월함수 : 대수적으로 구할수 없는 함수. 초월함수와 초등함수는 항상 같지 않음
* 지수함수, 로그함수, 삼각함수는 초등함수이면서 초월함수이기도 함(?)
=> 테일러 급수로 구할수 있어서 이들이 초등함수와 초월함수 둘다 포함되는건지 잘 모르겠음
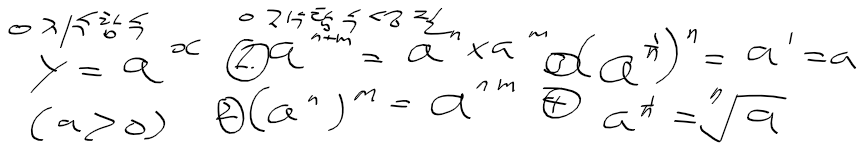
지수 함수
- 양의 상수 a( a > 0)이 주어질때 y = a^x인 함수
* 여기서 a가 왜 양수인 경우만 다루는지는 잘 모르겠음
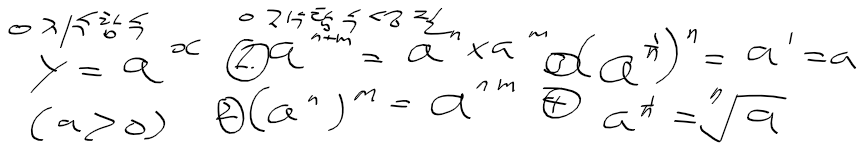
단조 증가와 단조 감소
- 지수함수는 a > 1인지 1 > a > 0 인지 여부에 따라 단조 증가, 단조 감소의 형태를 보임
- 추가로 지수 함수는 실수 전체에 정의되어 단조증가, 단조증가하나 치역(y 범위)는 양의 실수 공간임
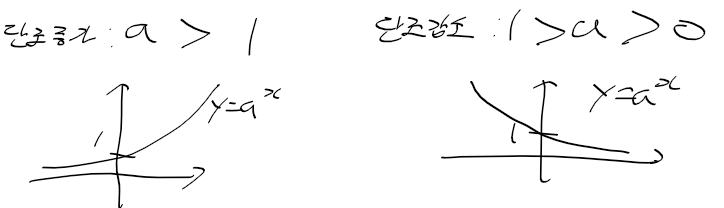
로그 함수
- 지수 함수를 역으로 하면 x = a^y를 만족하는 역함수가 존재함
- 로그 함수 : a를 밑(기저)로 하는 지수함수의 역함수
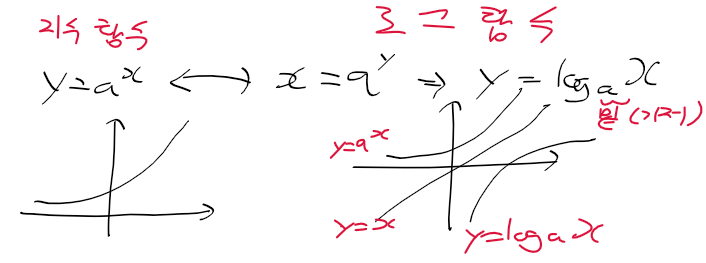
로그함수의 성질
- 로그 함수는 복잡한 곱샘 나눗셈을 단순한 덧셈, 뺄셈으로 변환해준다!
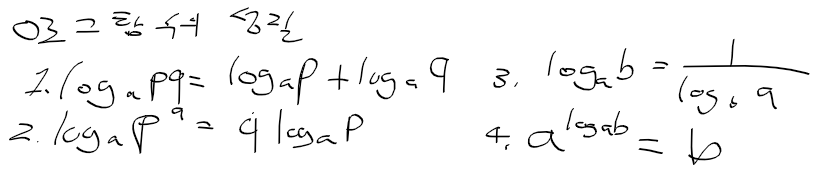
네이피어의 수
- 1에 가까워지는 1 + 1/x를 무한에 가까워지도록 x번 곱하면 (1 + 1/x)^x 했을때 수렴하는 수
- e = 2.712...
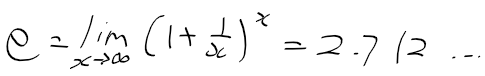
지수함수의 미분
- 도함수의 정의에 지수함수 f(x) = a^x를 대입하면 다음과 같이 지수함수의 도함수를 구할 수 있음
* 갑자기 f'(0)가 나오는 이유는 지수함수의 도함수식 x에다가 0을 대입하면 그대로 나오기 때문
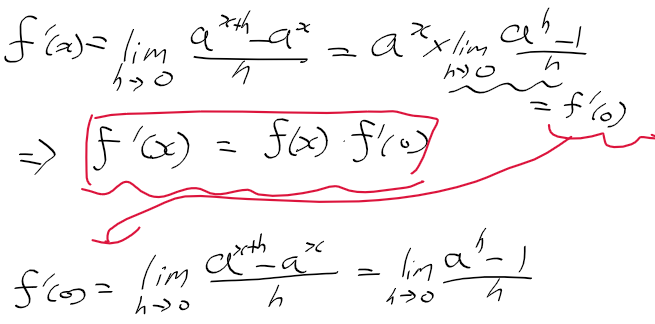
밑이 e인 지수함수의 미분이 자기자신인 이유
- 먼저 f'(0)에서 시작하자
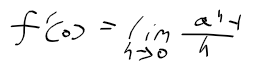
- 1) s = 1/(a^h - 1)를 정리하면 a^h = 1 + 1/s이 나온다. 이를 h에 대한 식으로 정리하자
- 2) s와 h에 대한 식을 f'(0)에 대입한다
- 3) f'(0) = 1/log_a_e가 나온다
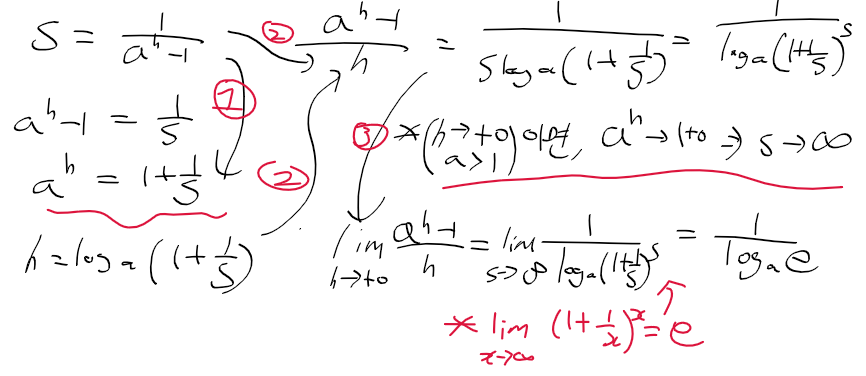
- 그러므로 지수함수 f(x)의 f'(0)는 log_e_a가 된다.
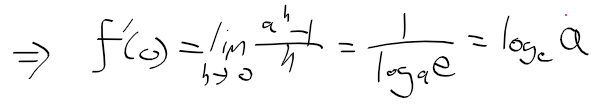
- 지수함수의 도함수 정리 결과에 a=e와 f'(0) = log_e_a를 대입하면 (e^x)' = e^x가 나온다
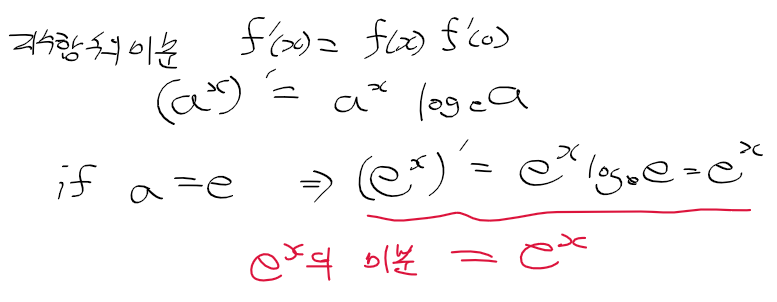
밑이 e인 지수함수와 역함수(자연로그)
- 지수함수의 역함수가 로그함수 이듯, 밑이 e인 지수함수의 경우에도 역함수는 로그
- 밑이 e인 로그함수를 자연로그라 부르며 ln x로 표기
- 밑이 e인 지수함수는 exp(x)로 표기
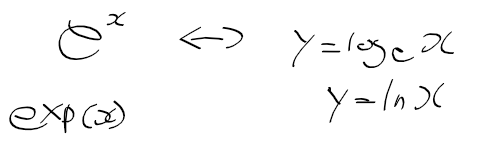
삼각함수와 도함수
- 반지름 길이가 1인 단위원과 0<= theta <= 2pi에서 x, y의 좌표
- 피타고라스 정리와 삼각함수 : cos^2 theta + sin^2 theta = 1
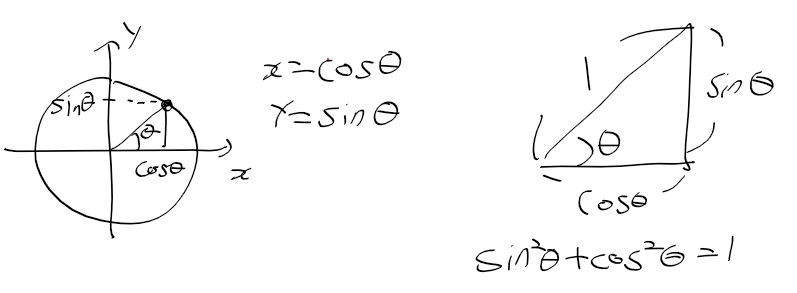
- 탄젠트 = 사인 / 코사인

- 삼각함수의 도함수 정리 하기 귀찬으므로 결과만 놓으면...
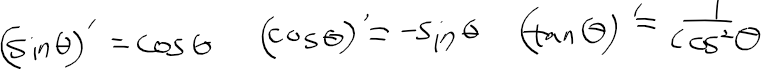
'수학 > 해석,기하' 카테고리의 다른 글
| 기초해석학 - 6. 테일러 근사와 해석 함수 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 5.무한소와 테일러 공식 (0) | 2023.09.21 |
| 기초해석학 - 3. 미적분 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |