멱급수
- 급수 : 수열의 합(유한급수 : 수열이 유한, 무한급수 : 수열이 무한)
- 멱급수 : 거듭제곱을 포함한 무한 급수
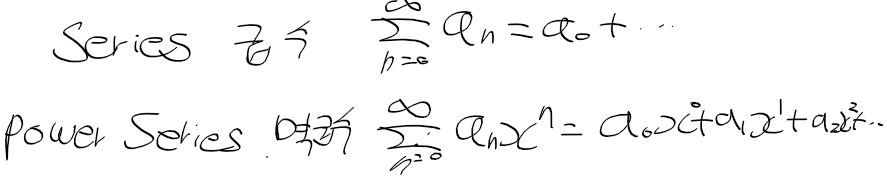
미분가능한 함수
- 연속미분가능 : 구간 I의 모든 점 x에서 미분 가능한 함수 f(x)는 다른말로 연속미분가능함
-> I에 미분가능한 모든 함수의 집합 C^1(I)는 다음과 같음(C1-급 함수)
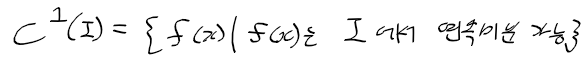
- 두번연속미분가능 : 도함수 f'(x)도 구간 I에서 미분 가능한 경우
-> I에서 두번미분가능한 모든함수의 집합 C^2(I)는 다음과 같음
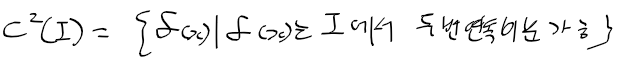
- m번 연속미분가능한 함수(m계 도함수)들의 집합을 다음과 같이 표현 가능하며 C 1 ~ m급 함수 집합은 다음 관계를 가짐
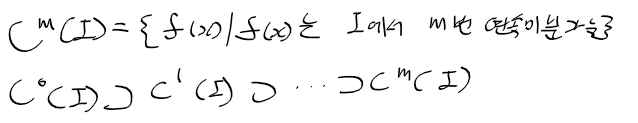
- 이런 집합의 교집합은 다음과 같음
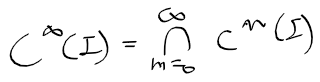
- 무한번 미분가능 함수 : C^inf-급 함수

일차 근사 되돌아보기
- 함수 f(x)를 x0에서 선형 근사한 일차함수가 (x1, f(x1))을 지나갈때 값 y는 다음과 같음(x0에서 미분계수는 alpha)
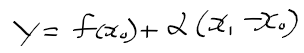
- 실제 f(x1)의 값과 일차 근사함수의 x1에서 값 차이를 g(x1)이라 하면 다음과 같음
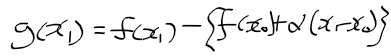
- 미분계수 alpha 대신 beta를 기울기로하고, (x1, f(x1))을 지나는 일차 함수 식은 다음과 같음
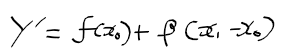
- 실제 f(x1)과 beta를 사용한 일차 함수 식의 값 차이를 h(x1)이라 하면 다음과 같다.
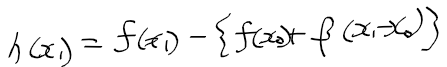
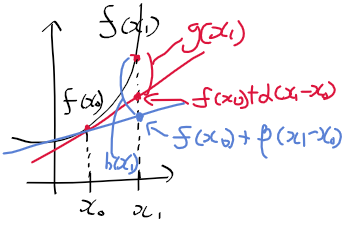
- 함수 f(x), g(x1), h(x1)의 관계는 다음과 같음
=> x1->x0으로 극한에서 g(x1)이 h(x1)보다 오차가 작음
=> x1 -> x0이 되어갈수록 g(x1)이 h(x1)보다 빠르게 0에 가까워진다!
=> alpha = f'(x0)이 최적의 1차 근사이다!
(beta를 기울기로 하는 선형 근사는 오차가 더 크므로)
무한소
- 무한소 개념
1) 모든 양수보다 작지만 0보다 큰 상태
2) 엡실론델타논법 존재전에 극한을 설명하기 위해 고안한 개념.
3) x->x0에서 무한소란? : x -> x0 극한에서 0 되는 함수f(x)
- 아래 g(x), h(x), g(x)/h(x)의 x->0 일때 값의 변화
=> g(x) = x^2가 가장 빠르게 0에 근접한다!

- 비교 가능 무한소 : 위 g(x), h(x)와 같이 특정한 값에 수렴하는 경우의 함수
- 동위 무한소 : 아래의 식에서 alpha != 0 인 경우

- 동치 무한소 : 위의 식에서 alpha = 1인경우, 동치관계라고도 함. 아래와 같이 두 함수사이 물결로 표현
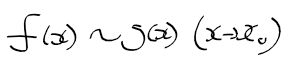
- 동위와 동치 무한소 : 동치무한소는 0에 수렴하는 속도가 같다! 동위 무한소는 수렴 속도가 상수배 다르다
- 무시가능 무한소 : 좌측 식처럼 f(x)가 g(x)보다 빨리 0에 수렴(분자가 먼저 0된다)하는 경우 f(x)는 g(x)의 무시가능무한소
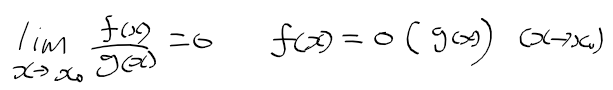
무시가능 무한소와 근사식
- f(x) = (x + 1) ^3, g(x) = x로 놓고 전개해보자
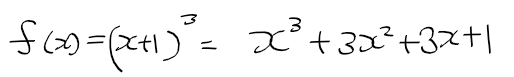
- lim f(x)/g(x) = 0을 성립시키기위해 f(x) - (1 + 3x)를 분자, g(x)=x를 넣으면 다음과 같이 정리된다.

- 즉 f(x) - (1+3x) = o(x)
=> x가 0에 가까워질 때 "f(x) - (1+3x)"는 x의 무시가능 무한소 o(x)가 된다.
* 이때 o(x) = x^3 + x^2로 1차보다 높은 항만으로 구성됨.
- o(x)를 제외하고 f(x)에 대한 식으로 정리하면, x가 0에 가까워질때 3x + 1란 1차 근사식이 나온다.

란다우 기호
- 위 식에서 무시가능무한소 o(x)에서 사용한 기호 o 혹은 O
- 리틀오 : o는 x보다 큰 차수 항들의 모임
- 빅오 : O(x)는 x를 포함하여 x보다 큰 차수 항들의 모임
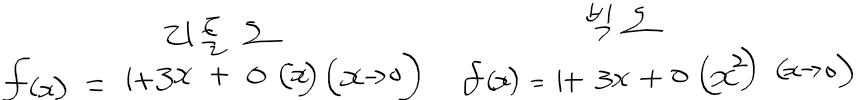
란다우 기호로 1차 근사 표현하기
- 아까 일차 근사 되돌아보기에서 그린 그래프를 다시 가져와서 보자

- x0 직선의 방정식에 x1을 대입하지 않고 x에 대한 식으로 나두면 다음과 같다

- 그러면 f(x)와 직선 방정식(대충 y라 하자)의 오차를 g(x)라 하였으므로, f(x)는 다음과 같이 정리할수 있다.
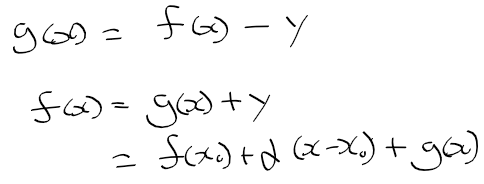
- 이 때 g(x)는 x-x0의 관계를 다음과 같이 정리할수 있다. 즉, g(x)는 "x-x0"에 대해 무시가능무한소
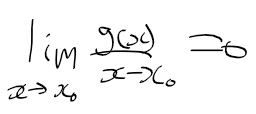
- f(x)를 란다우기호로 다시 정리하면 다음과 같이 되며 1차 근사로 다시 정리할수있다.
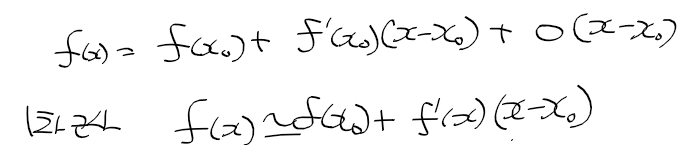
테일러 공식과 f(x)
- 테일러 공식으로 f(x)를 정리하면 다음과 같음
* 테일러 공식 : 폐구간 [x, x0]에서 f^(n-1) (x)가 연속이고 f^(n)이 존재시 다음 관계가 성립
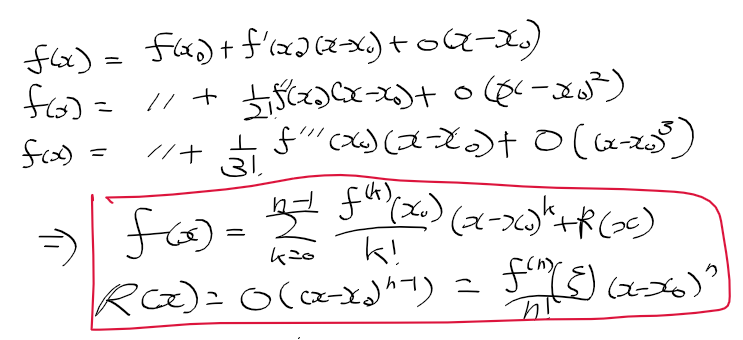
'수학 > 해석,기하' 카테고리의 다른 글
| 기초해석학 - 6. 테일러 근사와 해석 함수 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 4. 초등함수 (0) | 2023.09.19 |
| 기초해석학 - 3. 미적분 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |