깜지로 쓰려는 블로그

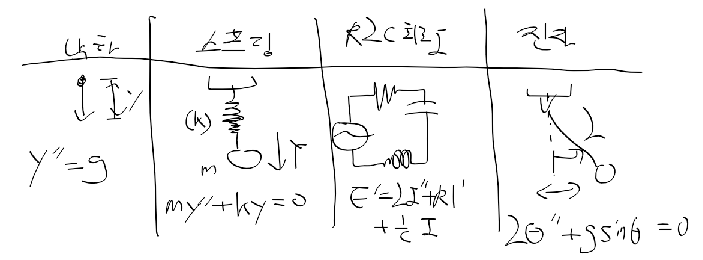
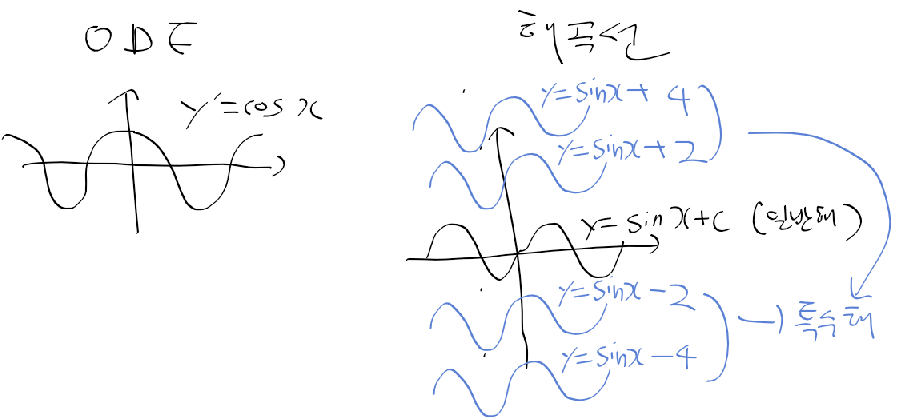
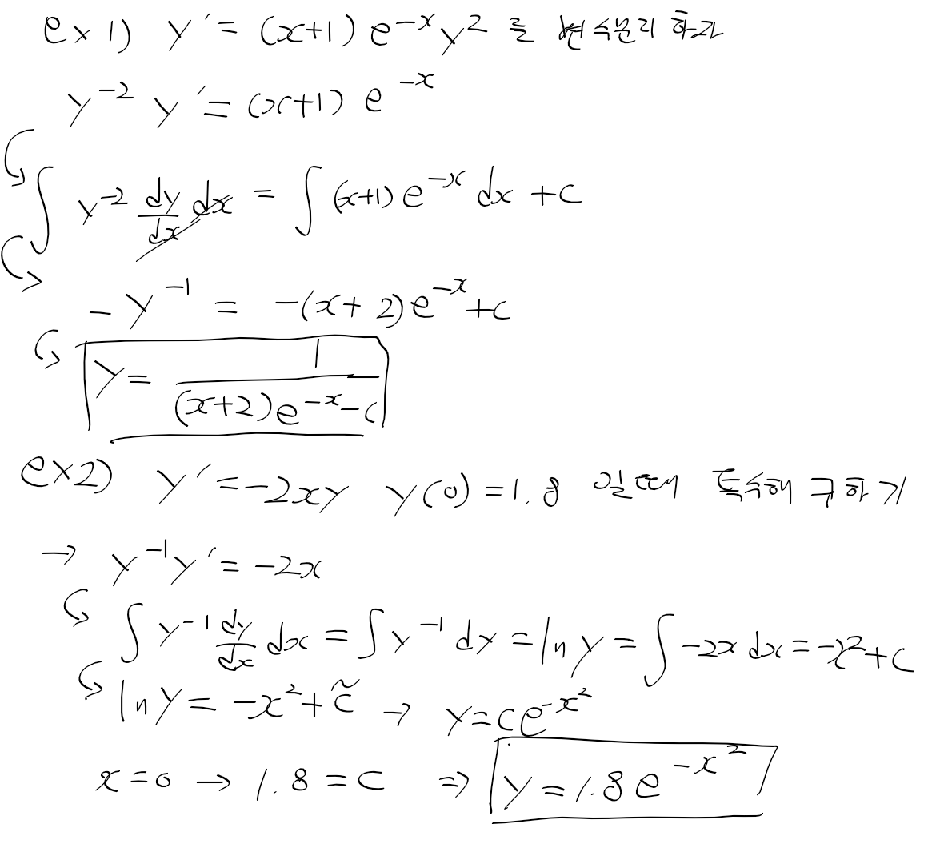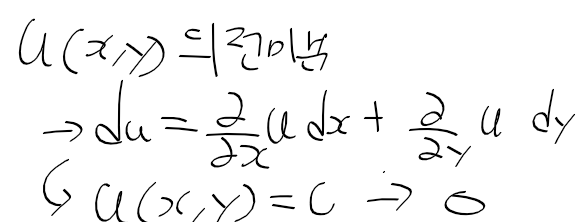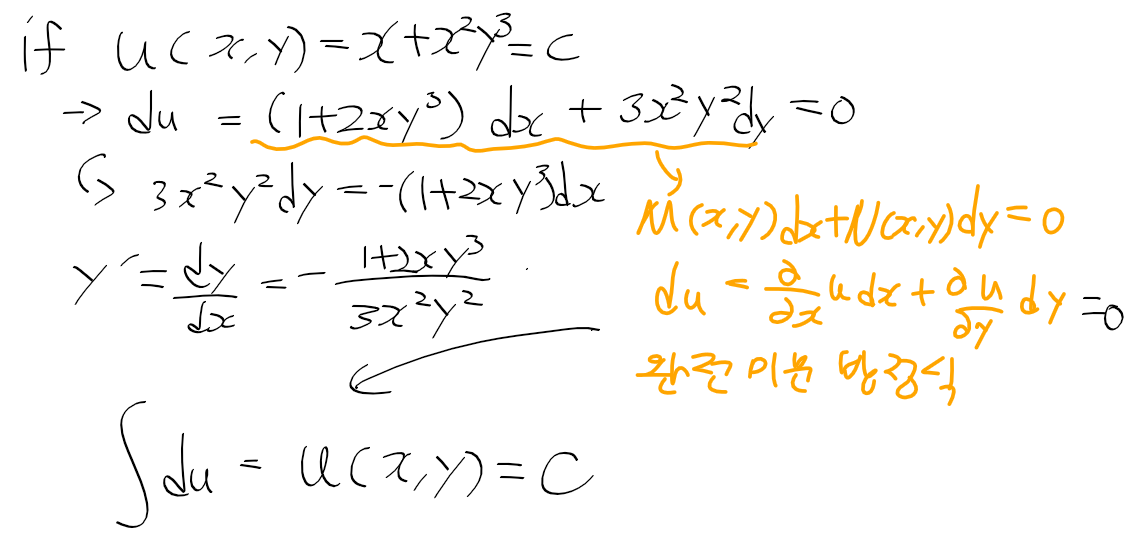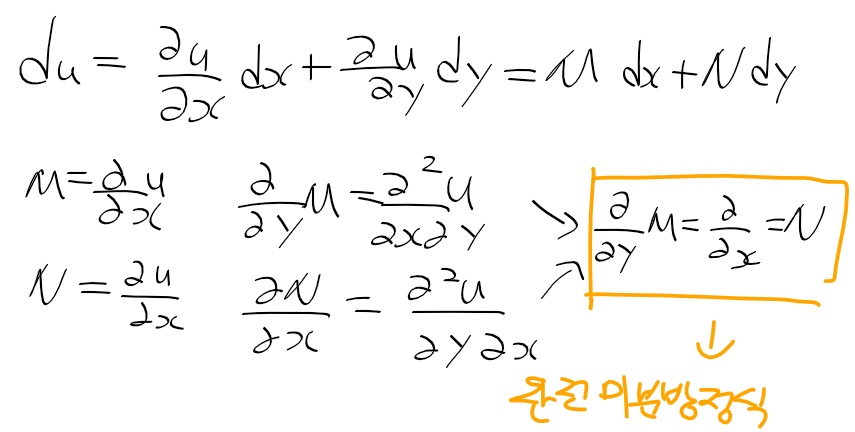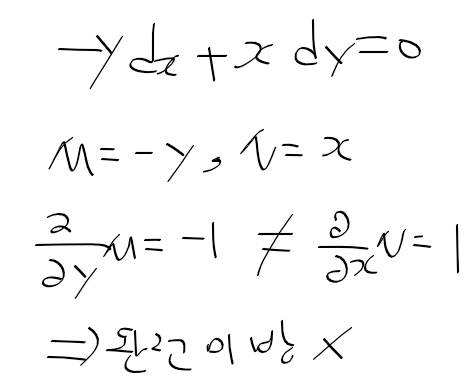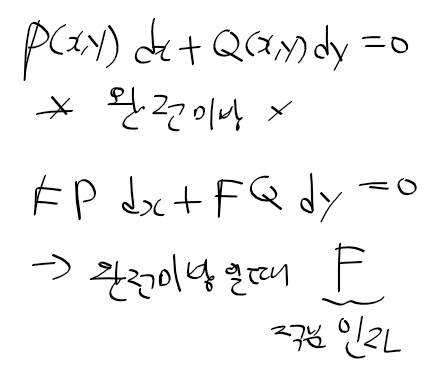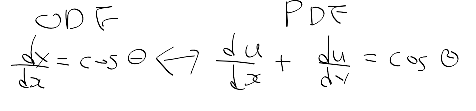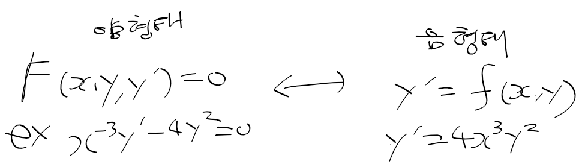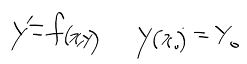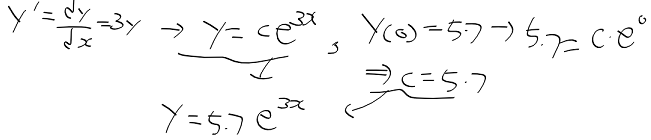애고 요새 하나만 깊게 하지 않고 이것 저것 일 벌리는게 많다.

최근에 이책 저책 읽기 시작하기 전부터 전기 자격증 준비하면서 공부하긴 했었는데

미적분 물리책을 보기 시작하면서 로봇 공학까지는 그래도 대강 다 보기는 했지만

그 뒤에 본책 메카트로닉스, 파이썬 프로그래밍, 인생 유니티 교과서, 오늘 보기 시작한 kreysig 공업수학까지는

한번에 다 보지도 못하고 봐야할 조금씩 본 책, 앞으로 봐야할 책들만 쌓고있다. 

이럴수 밖에 없는게 개론이나 쉬운 책이면 몰라도 지금 보고 있는 전문 서적은 대충 보고 끝낼수도 없고

최소한 이론은 정리하거나 실습은 해야 그래도 봤다고 할수 있을거고 그래야 남는게 있으니

시간이 오래걸리더라도 어쩔수가 없다.

그렇다고 한책만 깊게 보지않고 여러가지를 늘리고 있는데

한 책만 오래 보면 질리는 순간도 오고, 막힐때 그런걸 이해하기 위해서 다른 책부터 먼저 보는게 더 나은 경우도 많으며

결국에는 한 책에 나오는 내용이 딴 책에도 나오고 어렵게 나오는 표현이 더 이해하기 쉽게 표현한 경우도 꾀 있다보니

자꾸 다 읽은 책이 늘지 않고 보는 책만 늘어나고 있다.

딴건 몰라도 공업수학 책은 상, 하권 다읽으려면 3주이상은 걸릴거같아서 걱정이다.

------

아무튼 어제는 인생 유니티 교과서라는 책을 잠깐 봤었는데

프로그래밍 공부하면 3차원 공간에서 뭔가 만들어 보고싶다는 로망이 있었다.

그러다가 yes 24 북클럽 무료책에 이 책이 있길래 봤는데 정말 보물같은 책이었다.

지금 내가 학교 수업도 듣고, 공학 공부도 하다보니 실제로 유니티로 뭘 만들어볼 시간이나 여유가 전혀 없지만

이 책이 독자들을 안내하는 방식이 너무 마음에 들었다.

내가 지금까지 본 프로그래밍이나 다른 책들은 하나같이 지식, 실습을 나열했다고 해야될까?

아예 왜 하는지 알려주지도 않거나, 알려 준다 해도 학습에 동기를 불어넣어줄만큼 와닿지가 않는 책들이 많았다.

그렇지만 이 책의 경우에는 소개말부터가 정말 보물같았는데 내용도 정말 친절하다.

이 책에서는 유니티를 사용해서 게임을 만드는건 당연하지만

단순히 게임 만드는 방법을 알려줄 뿐만아니라

유니티 어플리케이션 설계 과정을 일반적인 알고리즘 책에서 알고리즘 설계 단계나

다른 CS 책에서의 소프트웨어 설계 단계처럼 딱딱하지 않고

실제 기업 환경에서 프로토타이핑하고, 알파 버전 만들고, 베타 버전을 만드는 과정을

설명하면서 어플리케이션을 만들다보니 딱딱한 책들보다는 더 와닿는다.

또한 파트별로 넘어갈때마다 내가 어디쯤에 와있는지 다음 파트에는 어느정도 가는지를 알려주는데

대부분의 책은 외워! 실습해! 지도도 주지 않고 앞으로 가!라고만 한다면

이 책은 앞으로 갈 방향이 어디인지, 어느정도 진도나가면 내가 어디쯤에있고, 다음에는 어디까지 갈것인지를

명확하게 설명해주니까 더 동기 부여된다고 해야될까 앞으로의 막연함, 막막함 같은게 줄어드는 느낌이들더라.

나는 책을 사기전에 꼭 인삿말을 보는 편인데, 

인삿말을 보면 저자가 이 책을 왜 썻는지, 어떤걸 목표로 하는지, 그냥 돈벌려고 했는지, 성의있게 썻는지

대강 감이 잡히기도 하고 공부하는 내용보다는 저자의 생각 철학을 보는게 더 재밋어서 자주본다.

이 책은 인삿말부터가 제목에다가 '쉽게 배우는'이니 '프로젝트'라면서 진짜 중요한 노하우는 없고

조금만 검색하면 나올 내용들을 파는 붕어빵같은 책들과는 다르다는 느낌은 많이 받았다.

아아 진짜 시간만 있으면 대충 읽어볼게 아니라 실습하면서 뭐라도 만들어 볼텐데

언제 여유있을진 모르겠지만 되면 해봐야지

변수분리법

- 다음과 같은 상미분 방정식(변수 분리 가능 방정식)이 주어질 때, 양변에 x로 적분을 하고 정리를 하면 좌변은 y만 우변은 x만 나오며 이를 계산하여 일반해를 얻는 방법

변수 분리법을 이용한 예제

편미분과 전미분

- 편미분 : 다변수 함수에서 한 변수만을 다루고 나머지 변수들은 상수로 취급한 미분 

 -> 한 변수가 변할때의 변화율

- 전미분 : 다변수 함수에서 모든 변수를 동시에 다루는 미분

 -> 모든 변수가 변할때의 변화율

전미분과 완전미분방정식

- 함수 u(x,y)의 편도함수가 연속일때 이 함수의 전미분은 다음가 같고, u(x, y)가 상수인 경우 전미분은 0이된다.

- u(x,y)가 아래와 같이 주어진 경우 전미분을 구하고, 미분방정식의 형태로 만들면 완전미분방정식이 나온다.

- 이 완전 미분방정식 du = 0이므로 적분을 하여 일반해를 구하면 u(x, y) = c의 형태로 음함수해가 된다.

완전미분방정식이 되기 위한 조건

- 완전미분방정식은 전미분 du = M(x, y)dx + N(x, y) dy 의 형태가 되야 하며 M과 N의 편도함수가 같을때 성립한다.

완전미분방정시 아닌 경우와 적분 인자

- 아래의 식은 완전 미분방정식이 되지 않음.

- 1/x^2을 곱할 시 

- 적분인자 : 방금 완전미방이 아닌 식에 1/x^2을 곱하여 완전미방으로 만든 것처럼 곱한 함수 F(x,y)가 적분인자.

미분 방정식 differential equation

- 현실의 물리 현상을 미분을 통해 모형화 한 방정식

- 상미분 방정식 ode ordinary de : 변수가 한개인 미방

- 편미분 방정식 pde partial de : 변수가 여러개인 미방

- 모델링 : 공학, 물리학, 화학 등 여러 분야의 실제 현상을 수학적으로 계산할 수 있도록 표현한 모델

* 목표 : 현실 문제에서상미분 방정식을 유도(모델링)하고, 방정식을 풀고 그래프 시각화하여 해석하자

1계 상미분 방정식

- 2차, 3차등 고차 도함수가 아닌 1차/1계 도함수만을 가지고 있는 미분방정식

공학 문제와 모델링

- 공학 문제를 계산을 통해 풀려면 수학 모델로 만들며 이를 모델링이라 함

- 모델링에 미방을 사용하는 이유 ? -> 다양한 물리 현상들이 도함수(미분)을 포함하고 있음(ex:속도, 가속도)

상미분방정식과 편미분 방정식

- 상미방 : 하나의 변수 <-> 편미방 : 여러 변수

미분 방정식 활용 예시

- 낙하, 스프링에서 변위, RLC 회로 전류, 진자 운동

상미분방정식의 양형태, 음형태

- 양형태 explicit form : 모든 항을 좌변으로 옮김

- 음형태 implicit from : 도함수만 좌변으로 옮김

해

- 해 : 어느 함수 h(x)가 열린 구간에서 정의/미분 가능하며, 이 함수 h(x)를 만족하는 y

- 해곡선 : 해들의 곡선

- 열린 구간 : a < x < b에서 양 끝 a와 b를 포함하지 않는 구간

상미분 방정식과 해

- y' = cos x인 (음형태) 상미분방정식이 있을때, ode의 해는 y = sin x + C

- 일반해 general solution : 임의의 상수 C를 가지고 있는 해

- 특수해 particular solution :  임의의 상수 C를 특정값으로 할때의 해

특수해와 초기값

- 초기조건 : 특정 입력값에 대한 출력 -> 일반해에 대입해 임의의 변수 c 값을 구할 수 있다.

 => 초기조건을 통해, 해당 초기조건의 특수해를 구한다.(초기값 문제)

초기값 문제 예시

- y' = 3y, y(0) = 5.7일 때 특수해를 구해보자

 * y' = 3y : y를 미분했더니 y가 나온다 y는 지수함수의 형태다.

 * 구한 일반해에 위 초기조건을 대입하여 C를 구하

=> 특수해 y = 5.7 e^3x

해석적 방법과 수치적 방법

- 해석적 방법 : 직접 계산하여 정확한 해를 구함

- 수치적 방법 : 근사화를 통해 해를 구함

1계 ode의 기하학적 의미

- y' = f(x, y)를 기하학적으로 해석해보자

- 점 (x0, y0)을 지나는 위 ode의 해곡선은 y'(x0) = f(x0, y0)을 만족해야한다.

 -> 그래픽 or 수치해석적 방법으로 ode의 근사해를 얻을 수 있다.

상미분 방정식의 방향장 시각화

- y' = y + x라는 상미분 방정식이 주어질 때, (0, 1), (0, 0), (0, -1) 세 점을 지난다면

 -> 3개의 해곡선을 가지며, 세 해곡선과 해당 ode의 방향장은 다음과 같다.

* 뒤에 오일러방법 계산하다가 자꾸 값이 이상하게 나왔는데 일반해부터 잘못 구한거같다

오일러 방법 - 간단한 수치해석적 방법

- ode와 초기값이 주어질 때, x1 = x0 + h라면

  => y1 = y0 + h * y' = y0 + h * f(x0, x0)

- 간격 h가 작을수록 오차는 줄어든다.

- h = 0.2로 놓고 구한 근사값과 실제 특이해를 비교하면 오차가 점점 커지는걸볼수있다.