추상대수학
- 대수 구조를 다루는 수학적 대상을 연구하는 분야 (체, 군, 환, 벡터, 경자 등)
- 연립 선형 방정식 해를 구하는 연구에서 행렬과 판별식 개념을 찾아냄 ->선형대수 생김
- n차 다항식 근을 구하는 공식 찾는 시도에서 군을 대칭의 대수적 표현으로 재발견
- 4차 or 그이상 차수의 디오판토스 방정식 산술 연구로 환과 아이디얼이란 개념이 생김
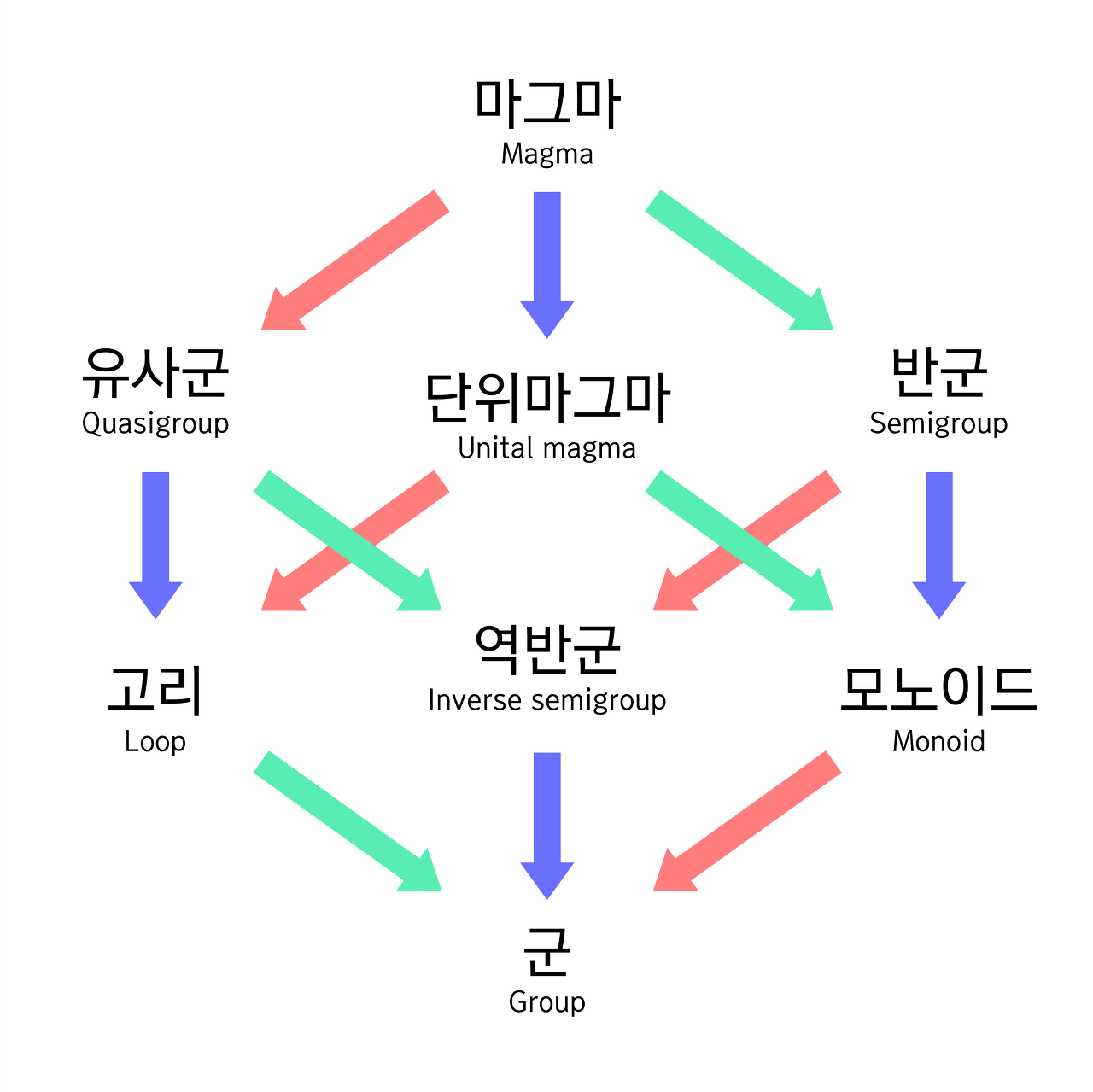
추상대수학
- 대수 구조를 다루는 수학적 대상을 연구하는 분야 (체, 군, 환, 벡터, 경자 등)
- 연립 선형 방정식 해를 구하는 연구에서 행렬과 판별식 개념을 찾아냄 ->선형대수 생김
- n차 다항식 근을 구하는 공식 찾는 시도에서 군을 대칭의 대수적 표현으로 재발견
- 4차 or 그이상 차수의 디오판토스 방정식 산술 연구로 환과 아이디얼이란 개념이 생김

대수학
- 공리를 만족하는 수학 구조의 성질을 연구함??
- 이라고 하는데 방정식같은거에 수나기호로 문제를 푸는게 대수학이 아닌가
- 알 콰리즈미가 수 대신 문자를 쓰면서 방정식을 푸는 것에서 나옴
프랑수아 비에트 전후의 대수학
- 프랑수아 비에트 이전의 대수학은 '계산방법'과 '다항방정식의 해를 구하는방법'을 다루었으니 계산하는 것이 맞았었다.
- 프랑수아 비에트가 처음으로 변수(로마자 미지수 사용)의 개념을 사용하기 시작해서부터 논리로 연산의 성질을 찾는 학문이 됨(현대 대수학)
* 프랑수아 비에트는 근과 계수의 관계를 찾아내었으며, 원주율로 무한급수를 찾아냄
현대 대수학
- 추상적인 성질로 정의되는 구조, 대수 구조를 연구하는 분야
- 대수 구조의 예시 : 군, 환, 체, 벡터공간, 격자
해석학
- 대수학과 기하학에 미적분을 사용해서 함수의 연속성을 연구하여 형식화하는 학문
=> 수열, 극한, 급수, 해석함수 등이 나옴
- 분야
- 실해석학 : 실변수 함수를 미적분함.
- 함수해석학 : 함수 공간 다룸, 힐베르트 공간 등
- 조화 해석학 : 푸리에 급수 & 추상화한것 다룸
- 복소 해석학 : 복소 변수 함수 다룸
- 미분기하학 : 미적분을 공간에 적용
- 수치해석 : 문제를 알고리즘으로 근사해서 다룸
테일러 급수를 이용한 근사
- 다항식 차수가 높아 질수록 더 넓은 범위로 근사값이 가까워 진다!
=> 테일러 급수는 연속미분가능함수를 n차 다항식으로 만들어 줄수 있음
=> n -> inf가 될때 얼마나 f(x)와 일치할까? 함수열의 수렴을 보아야함
- ln(1 + x)를 테일러 급수로 근사화한 모습
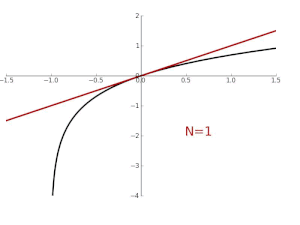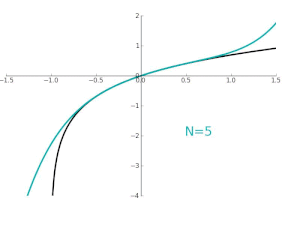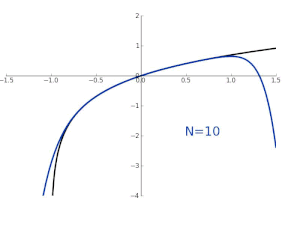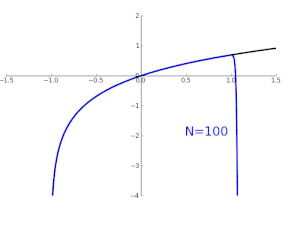
- 지수함수 y = e^x를 테일러 급수로 근사한 모습
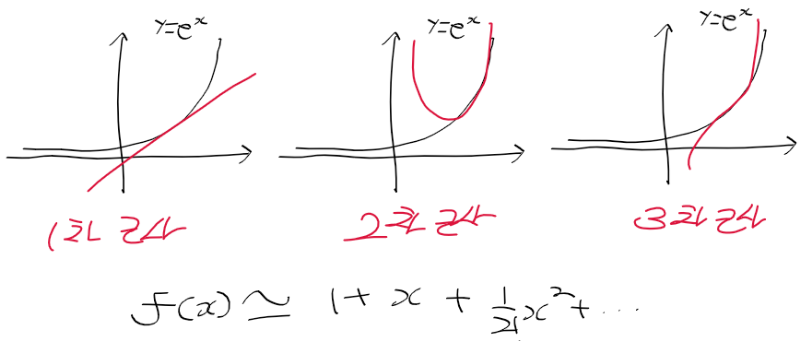
점멸수렴과 균등 수렴
- 점멸 수렴 : 구간 I의 함수열 fn(x)들이, 구간 I의 점 x0에 f(x)로 수렴하는 경우.
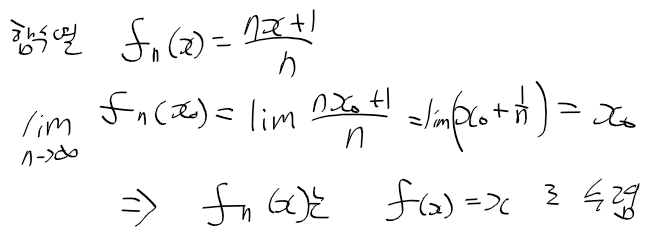
- 균등 수렴 : 함수열 fn(x) - f(x)의 차이 상한이 0으로 수렴하는 경우
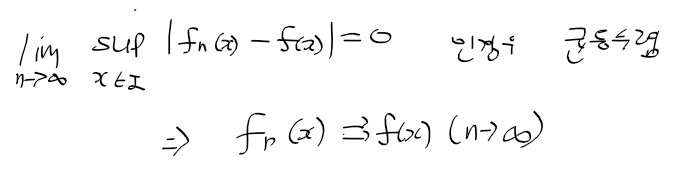
무한급수와 함수항 급수, 정급수
- 함수열 급수 : 함수열로 구성된 함수열
ex) 함수열 u_n(x)로 f_n(x)를 정의한 경우
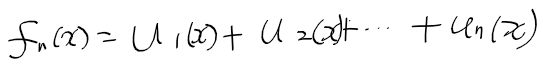
- 무한 급수와 함수항 급수 차이 : 무한 급수의 각 값이 값 대신 함수인 경우
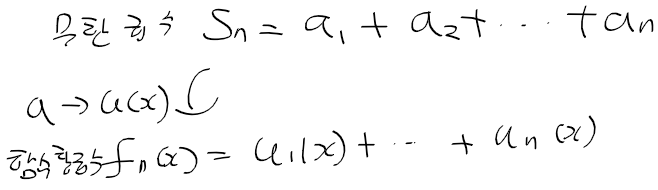
- 정 급수 : 다음의 모습을 띄는 함수항 급수, x0은 정급수의 중심

해석함수, 테일러 전개, 메클로린 전개
- 수렴 반경 :정급수 f(x)가 x0로부터 수렴할수있게 하는 범위
- 해석 함수 : 수렴 반경 r > 0인 정급수 f(x)가 임의의 점 x0에 대해 표현할 수 있는 경우 f(x)는 해석함수
(= 테일러 전개)
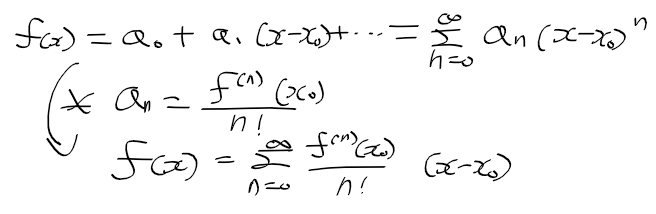
- 메클로린 전개 : 테일러 전개에서 x0 = 0인 경우
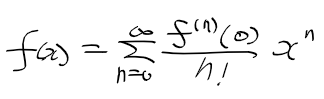
| 기초해석학 - 5.무한소와 테일러 공식 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 4. 초등함수 (0) | 2023.09.19 |
| 기초해석학 - 3. 미적분 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |
이번에 본 책은 만화로 쉽게배우는 시리즈의 푸리에 해석편이다.
푸리에 변환, 해석
처음 봤던게 신호와 시스템을 공부하면서 봤었는데
시간 영역의 신호를 주파수 영역으로 변환하는 것이고,
푸리에 급수로 푸리에 변환, 반대의 경우 역변환 공식가지고 이런저런 예제 풀곤 했었다.
그치만 그때 봤던 교재가 한빛 아카데미의 교재였는데
신호의 종류, 급수, 변환의 종류를 나열해놓고 위키백과보다는 조금 나은 정도의 설명이었지
왜 이렇게 하는것인지 이런 식이 왜 나온 것인지에 대한 설명은 부족한 정보가 나열된 책이라
처음 배우는 입장에서는 억지로 외우는 수밖에 없었다
처음 새로운 분야를 공부하면 뭐가 있는지 보기도 급급한데 뒷배경까지 관심가질 여유가 없는게 당연했다만
억지로 외워서 문제풀고다니다보니 지금은 거의다 잊은 상태
아무튼 이런 생각으로 푸리에 변환이 어떻게 만들어지고, 어쩌다 이런 형태가 되었는지 궁금하긴 했었는데
만화로 쉽게 배우는 푸리에 해석에서 일반적인 수학책처럼 복잡한 증명 과정은 없이
삼각함수와 미적분을 이해하고 있으면 푸리에 변환을 이해할수 있을 만큼 내용 흐름을 전개해 나간다.
여전히 나는 해석이란 단어를 모호하게 느꼈는데
푸리에 해석은 시간 영역에 대한 신호를 주파수영역으로 바꾸는 것인데, 푸리에 변환으로 얻은주파수 스펙트럼을 보고 신호의 특성을 알아내는 것이 푸리에 해석이었다.
푸리에 변환은 푸리에가 열전도현상을 연구하다가 아주 복잡한 파형이 단순한 파형의 합임을 알아낸것이고, 이후 삼각함수들의 급수 형태로 푸리에 변환의 수학적 형태가 만들어지게 되었다.
결국 푸리에 급수 - 삼각함수들의 급수로 모든 신호를 표현할수 있다고 하는데, 주기 신호를 다루는 푸리에 변화는 실제 시간에 따라 변하는 전체 신호를 할수는 없지만 일부 구간씩 잘라서 푸리에 변환으로 주파수들을 분할해 나가는걸 알수 있었고, 이 과정에서 이전에 오실로스코프로 찍어보았던 삼각파와 펄스파가 어떻게 푸리에 급수로 표현해내는지 보면서 조금은 전보단 와닿을수 있었음
https://www.yes24.com/Product/Goods/6175991
만화로 쉽게 배우는 푸리에 해석 - 예스24
세 명의 학생이 학교의 축제에 라이브 공연에 참가하는데 밴드의 보컬이 없다.푸리에 해석을 이용하여 보컬을 구하려는데…혜미, 예린, 지우는 같은 학교를 다니는 학생이다. 작사, 작곡을 잘
www.yes24.com
| 달콤한수학사1 탈레스의 증명부터 피보나치의 수열까지 (0) | 2023.09.22 |
|---|---|
| 프로그래머를 위한 기초 해석학 (0) | 2023.09.21 |
| 만화로 쉽게 배우는 미분방정식 (0) | 2023.09.20 |
| 사영기하학, 위상수학 (0) | 2023.09.19 |
| 테일러급수, 유클리드 vs 비유클리드, 수학의 정의, 갈루아 등 (0) | 2023.09.18 |
멱급수
- 급수 : 수열의 합(유한급수 : 수열이 유한, 무한급수 : 수열이 무한)
- 멱급수 : 거듭제곱을 포함한 무한 급수
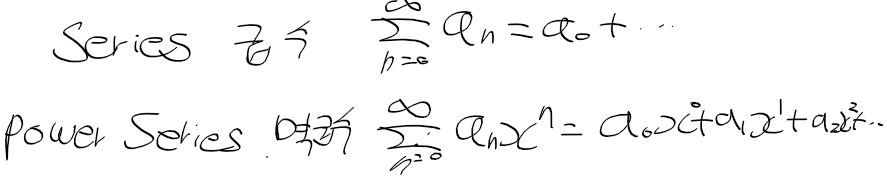
미분가능한 함수
- 연속미분가능 : 구간 I의 모든 점 x에서 미분 가능한 함수 f(x)는 다른말로 연속미분가능함
-> I에 미분가능한 모든 함수의 집합 C^1(I)는 다음과 같음(C1-급 함수)
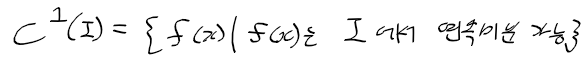
- 두번연속미분가능 : 도함수 f'(x)도 구간 I에서 미분 가능한 경우
-> I에서 두번미분가능한 모든함수의 집합 C^2(I)는 다음과 같음
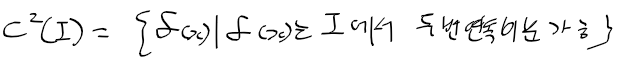
- m번 연속미분가능한 함수(m계 도함수)들의 집합을 다음과 같이 표현 가능하며 C 1 ~ m급 함수 집합은 다음 관계를 가짐
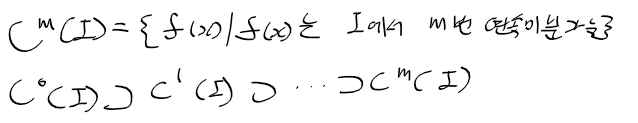
- 이런 집합의 교집합은 다음과 같음
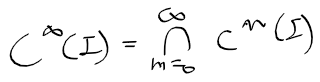
- 무한번 미분가능 함수 : C^inf-급 함수

일차 근사 되돌아보기
- 함수 f(x)를 x0에서 선형 근사한 일차함수가 (x1, f(x1))을 지나갈때 값 y는 다음과 같음(x0에서 미분계수는 alpha)
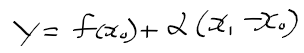
- 실제 f(x1)의 값과 일차 근사함수의 x1에서 값 차이를 g(x1)이라 하면 다음과 같음
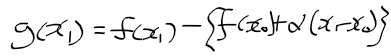
- 미분계수 alpha 대신 beta를 기울기로하고, (x1, f(x1))을 지나는 일차 함수 식은 다음과 같음
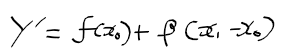
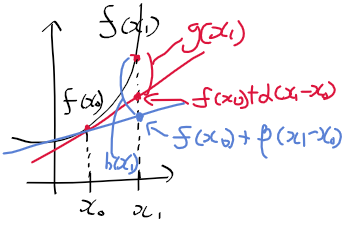
- 실제 f(x1)과 beta를 사용한 일차 함수 식의 값 차이를 h(x1)이라 하면 다음과 같다.
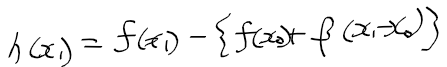
- 함수 f(x), g(x1), h(x1)의 관계는 다음과 같음
=> x1->x0으로 극한에서 g(x1)이 h(x1)보다 오차가 작음
=> x1 -> x0이 되어갈수록 g(x1)이 h(x1)보다 빠르게 0에 가까워진다!
=> alpha = f'(x0)이 최적의 1차 근사이다!
(beta를 기울기로 하는 선형 근사는 오차가 더 크므로)
무한소
- 무한소 개념
1) 모든 양수보다 작지만 0보다 큰 상태
2) 엡실론델타논법 존재전에 극한을 설명하기 위해 고안한 개념.
3) x->x0에서 무한소란? : x -> x0 극한에서 0 되는 함수f(x)
- 아래 g(x), h(x), g(x)/h(x)의 x->0 일때 값의 변화
=> g(x) = x^2가 가장 빠르게 0에 근접한다!

- 비교 가능 무한소 : 위 g(x), h(x)와 같이 특정한 값에 수렴하는 경우의 함수
- 동위 무한소 : 아래의 식에서 alpha != 0 인 경우

- 동치 무한소 : 위의 식에서 alpha = 1인경우, 동치관계라고도 함. 아래와 같이 두 함수사이 물결로 표현
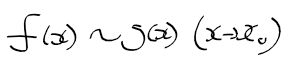
- 동위와 동치 무한소 : 동치무한소는 0에 수렴하는 속도가 같다! 동위 무한소는 수렴 속도가 상수배 다르다
- 무시가능 무한소 : 좌측 식처럼 f(x)가 g(x)보다 빨리 0에 수렴(분자가 먼저 0된다)하는 경우 f(x)는 g(x)의 무시가능무한소
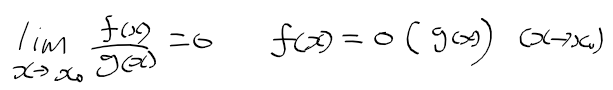
무시가능 무한소와 근사식
- f(x) = (x + 1) ^3, g(x) = x로 놓고 전개해보자
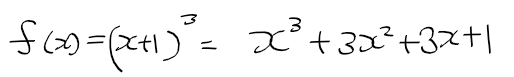
- lim f(x)/g(x) = 0을 성립시키기위해 f(x) - (1 + 3x)를 분자, g(x)=x를 넣으면 다음과 같이 정리된다.

- 즉 f(x) - (1+3x) = o(x)
=> x가 0에 가까워질 때 "f(x) - (1+3x)"는 x의 무시가능 무한소 o(x)가 된다.
* 이때 o(x) = x^3 + x^2로 1차보다 높은 항만으로 구성됨.
- o(x)를 제외하고 f(x)에 대한 식으로 정리하면, x가 0에 가까워질때 3x + 1란 1차 근사식이 나온다.

란다우 기호
- 위 식에서 무시가능무한소 o(x)에서 사용한 기호 o 혹은 O
- 리틀오 : o는 x보다 큰 차수 항들의 모임
- 빅오 : O(x)는 x를 포함하여 x보다 큰 차수 항들의 모임
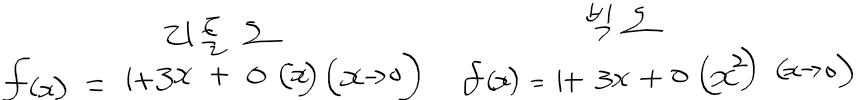
란다우 기호로 1차 근사 표현하기
- 아까 일차 근사 되돌아보기에서 그린 그래프를 다시 가져와서 보자

- x0 직선의 방정식에 x1을 대입하지 않고 x에 대한 식으로 나두면 다음과 같다

- 그러면 f(x)와 직선 방정식(대충 y라 하자)의 오차를 g(x)라 하였으므로, f(x)는 다음과 같이 정리할수 있다.
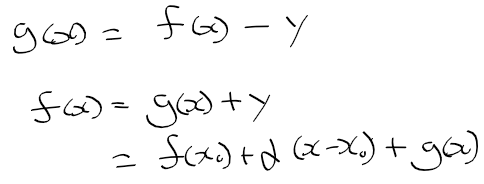
- 이 때 g(x)는 x-x0의 관계를 다음과 같이 정리할수 있다. 즉, g(x)는 "x-x0"에 대해 무시가능무한소
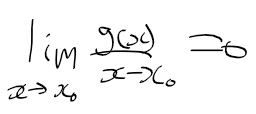
- f(x)를 란다우기호로 다시 정리하면 다음과 같이 되며 1차 근사로 다시 정리할수있다.
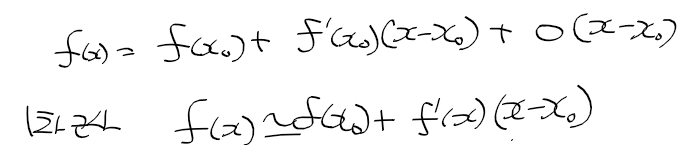
테일러 공식과 f(x)
- 테일러 공식으로 f(x)를 정리하면 다음과 같음
* 테일러 공식 : 폐구간 [x, x0]에서 f^(n-1) (x)가 연속이고 f^(n)이 존재시 다음 관계가 성립
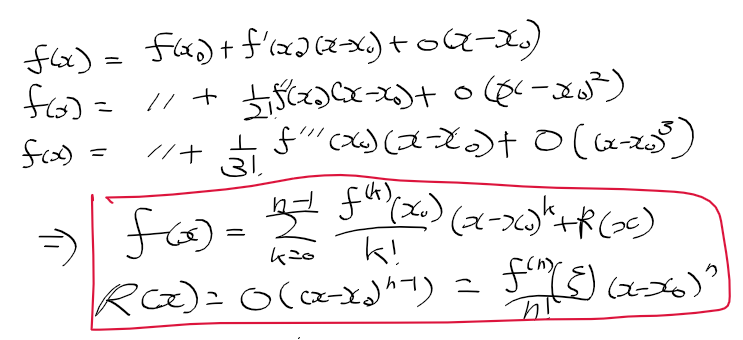
| 기초해석학 - 6. 테일러 근사와 해석 함수 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 4. 초등함수 (0) | 2023.09.19 |
| 기초해석학 - 3. 미적분 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |
이전 글에서는 대충 미분 방정식이 무엇이고
종류와 각 미방이 어떤 현실의 현상을 표현하고 있는지 간단하게 정리했다.
이번에는 실제 미방을 풀어내는 과정을 다뤄보려고 한다.
1. 일정 비율(mu)로 증가하는 종의 개체수 구하기
2. 구름 물방울이 떨어지는 속도 구하기
* 블로그에 latex 인가 뭐 스크립트 넣으면 그리스어 변환되기는 한데 넣기 귀찬아서 mu라 대충 적음
일정 비율(mu)로 증가하는 종의 개체수를 미방으로 풀어보기(변수분리법 사용하기)
- 대충 토끼의 경우 많으나 적으나 일정 비율로 증가한다고 가정하자
- 토끼가 적으면 적지만 (적은 개체수 x mu)만큼 증가하고 많은데로 (많은 개채수 x mu) 증가한다. 이를 미방을 표현하면 다음과 같다
* 여기서 말하는 일정 비율 mu는 현실의 데이터로 가장 적당한 값을 구해서 쓰면된다. 적당한게 없으니 그냥 변수로 놓자
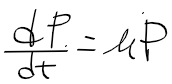
- 이 미방으로부터 해 P 그러니까 P(t)를 구하기 위해 우선 우항의 P를 좌항으로 보내주자.
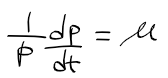
- 좌측 항에 dp와 dt가 붙어있다. 이 변수들을 이렇게 분리시켜보자(변수분리법)
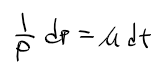
- 여기서 부정적분을 한 후 계산하면 다음과 같이 정리된다.

- ln P = ut + C이므로 이를 P에 대한 식으로 고쳐주면, 미분방정식의 해 P(=P(t))가 나온다.
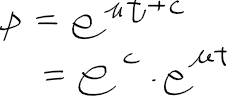
- 여기에 e^c를 대충 처음 인구수(초기조건) P0라 한다면 다음과 같이 정리된다
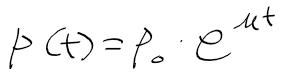
- mu가 0보다 크면 mu만큼 지수적으로 증가할것이고, mu가 0보다 작으면 인구는 줄어들것
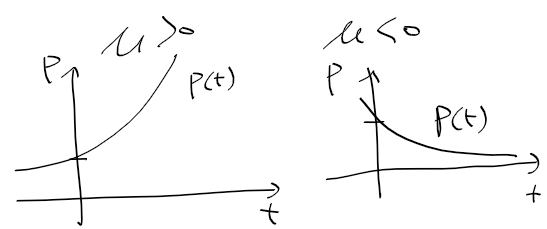
mu비율 만큼 증가하는 개체수 모델의 문제
- 방금 모델링한 미방의 해를 보면 지수적으로 증가하나 실제 종은 지수적으로 증가하다가 한계에 도달하므로 현실을 완벽히 반영못함
=> 현실을 잘 반영하는 미방 모델을 설계해야한다.
미정 계수법
- 비동차 미분방정식의 해를 구하는 방법으로 미정-정해지지않은 계수를 구하는 방법
- 대충 비동차 미분방정식, 우항이 0이 아닌 미방을 푸는데 사용된다 정도만 이해하고 넘어가자
떨어지는 물체의 속도와 빗방울이 만나는 저항
- 중력을 몰랐을 시절 아리스토텔레스는 무거운 물체일수록 빠른 속도로 떨어진다고 생각하였으나, 진공을 가정 시(저항이 존재하지 않는다면) 모두 떨어지는 속도가 같음
- 빗방울 저항 : 하늘에서 떨어지는 빗방울에는 점성(끈끈이) 저항과 관성 저항(공기와 부딪혀 생김)이 반영
* 적당한 그림 찾아보려 했는데 안보인다 ㅜㅜ
하늘에서 떨어지는 물체의 속도를 구하는 미분 방정식을 구해보자
- 속도는 아래 방향을 향하고, 물체에 작용하는 중력도 아래 <-> 저항력은 반대를 향한다. 그림으로 하면 다음과 같다.
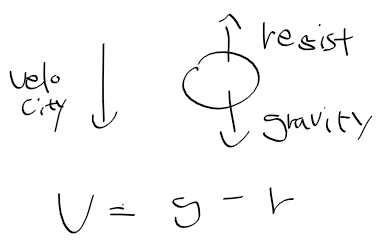
- 위에서 속도 v = 중력 g - 저항 r 이라 적긴 했는데 대충 적은 것일 뿐이고 ma = F로 제대로 표현해야한다.
- 여기서 외력 F는 중력 - 저항이긴 한데 저항은 점성 저항, 관성 저항으로 나누어서 표현하면 다음과 같다.
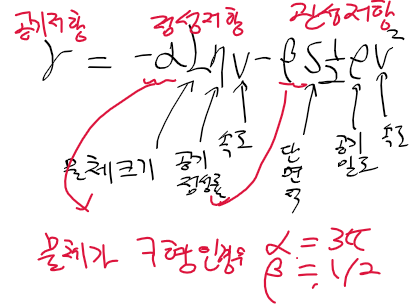
- 물체의 크기 L은 지름 2r, 단면적 S는 구의 면적 pi r^2이라 한다면 공기 저항은 다음과 같이 정리할 수 있다.
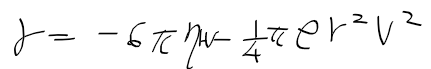
- 빗방울에 작용하는 힘 F = 중력 - 저항이므로 다음과 같이 정리할 수 있음
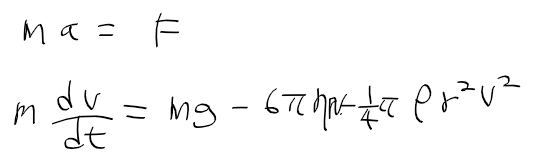
- 이걸 그대로 계산하기는 너무 복잡하므로 다음 두 경우로 나누어서 생각해보자
1) 구름 물방울 : 아주 작으므로 점성 저항만 작용된다
2) 빗방울 : 무거워 빨리 떨어지므로 관성 저항만 작용된다.
* 작을수록 점성저항, 클수록 관성 저항의 영향이 크다.
(비동차 미방 풀기) 구름 물방울이 떨어지는 속도 구하기
1) 우항이 0이일때의 해 일반해를 구한다
2) 일반해와 초기조건을 이용하여 특수해를 구한다
- 구름 물방울은 빗방울에 작으므로 미방을 다음과 같이 정리하자
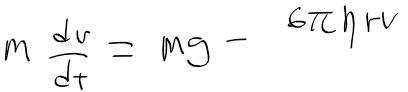
- 좌우항을 질량 m으로 나눈 후, 우항 v의 계수 6 * pi * r /m이 너무 복잡하므로 A로 놓으면 다음과 같이 정리됨.
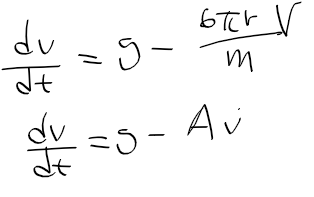
- v가 붙어있지 않은 g를 제외하고 모두 우항으로 보내면 비동차 미분방정식임을 알수 있다.
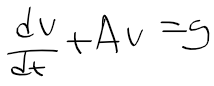
- 비동차 미분방정식을 풀기위해 g를 0으로 놓고 일반해부터 구하자
(마지막 e^c는 그냥 c로 놓자)
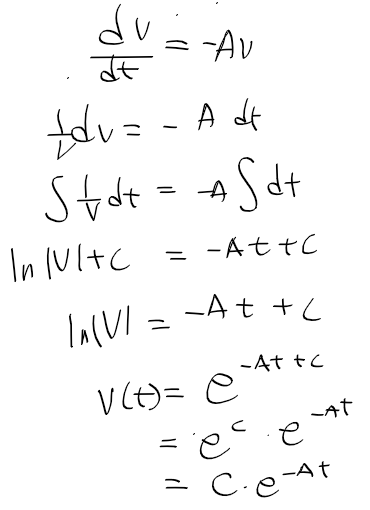
- 기존 미방에 다시 돌아와 v(t) = c * e^(-At)에서 c = c(t)로 놓고, 일반해 v(t) = c(t) * e^(-At)를 대입해서 풀어보자
- 좌항을 두 함수 곱의 미분 정리로 풀면 아래와 같이 정리된다.
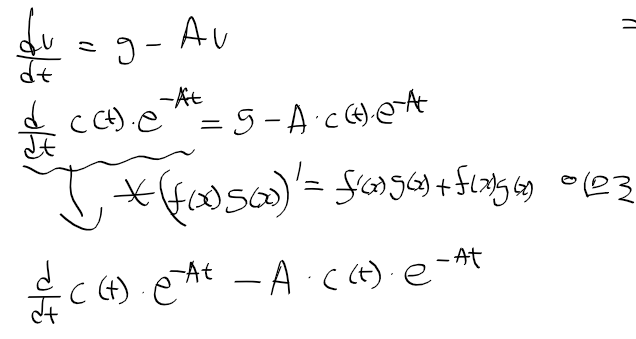
- 대입한 후 정리하면 c(t)에 대한 식이 만들어 진다.
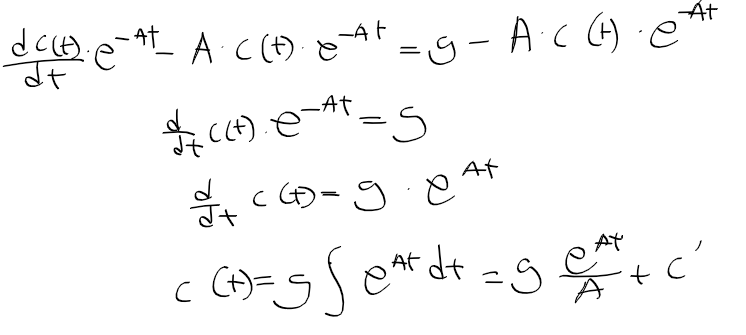
- 구한 c(t)를 원래 일반해 v(t) = c(t) * e^(-At)에다 대입하면, 시간 흐름에 대한 속도 변화 v(t)가 나온다.
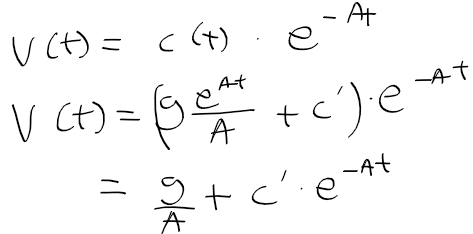
- 초기속도 v(0) = 0으로 하여 c'를 구한뒤 다시 v(t)를 정리하면 다음과 같음
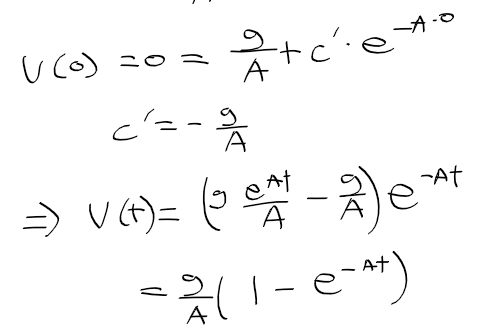
- 결국에 v(t)는 어떤 그래프 모양이 될까? 아무것도 정해진게 없으니 구할수는 없지만 지수함수 e^x와 e^-x의 형태를 생각해보자
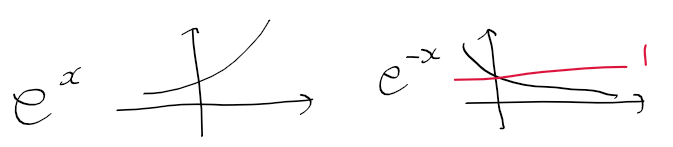
- 1-e^-x는 결국 0에서 시작해서 처음엔 빠르게 오르다 1에 가까워질 것이다
(e^-x 는 0에 수렴하므로)
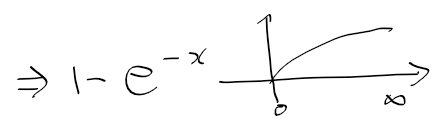
- 여기서 시간이 무한히 흐를때 최종적으로 가까워지는 속도를 종단 속도라 한다.
- t = 무한대로 놓고, 계속 나두던 A도 정리해보자
=> 결국 종단 속도는 mg(=중량)에 따라 정해진다!
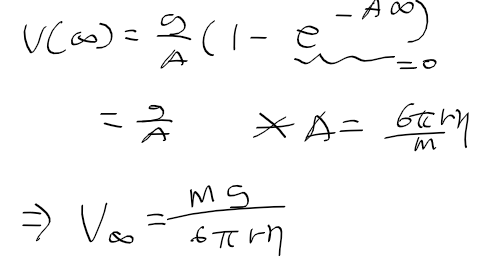
| 미분방정식으로 현실을 어떻게 수학 모델로 만들까 1 - 간단미방종류 (0) | 2023.09.20 |
|---|---|
| 컴퓨터 과학 관련 용어 1. 인코딩, 데이터 규격, 프로세서 관련 (0) | 2022.05.30 |
| 네트워크 간단 요약 (0) | 2022.05.29 |
| 로봇 공학 요약 - 로봇 종류부터 구성 요소, 구동기, 센서까지 (0) | 2022.05.05 |
미분 방정식
- 단순 정의 : 함수와 함수의 도함수로 이루어진 방정식
- 독립변수 개수로 분류한다면
1) 상미분 방정식 : 독립 변수가 하나인 미방
2) 편미분 방정식 : 독립 변수가 여러개인 미방
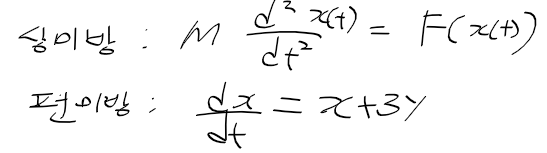
- 용도 : 운동 방정식 F = ma에서 시작해 현실 일을 미분 방정식의 형태로 표현 -> 해를 구한다 -> 현상 시뮬레이션이 가능
단순 예시) 비행기 시뮬레이션, 용수철 운동, 포물선 운동 등에서 시간 t에서 물체의 위치 같은것..?
+ 인구 변화, 광고 효과, 상품 매출 등을 미래에 어떻게 될지 예측 가능!
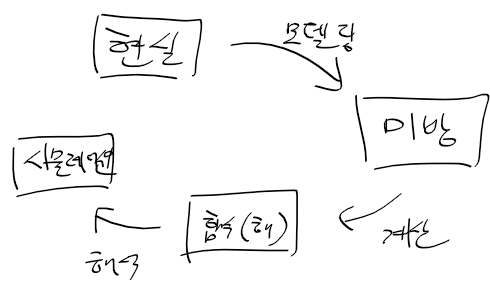
비행기 시뮬레이션 예제 - 비행기를 점으로 볼때, 등속 운동하는 비행기의 위치 구하기
- 실제 비행기에 구조와 작용하는 힘을 고려하기는 힘드니 점으로 볼때 위치를 구해보자
- 뉴턴의 운동 방정식 F = ma에서 시작
- 비행기가 등속운동하는 경우 외부의 힘이 존재하지 않음 ma = 0
- 가속도 a는 위치 x를 두번 미분한것이므로 다음과 같이 표현 가능
=> 다음 미방으로 부터 해인 x를 구하자, x는 시간 흐름에 따라 위치를 나타내는 함수(= x(t))
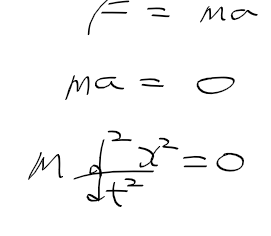
- 하지만 미방을 풀기전에, 거리 x = 시간 t X 속도 v 로 원래부터 이미 x(t)가 무엇인지 알고 있었다.
- x(t)에다가 초기 시작위치 x_0를 추가해주면 다음과 같이 정리됨
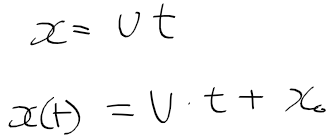
- 10m 지점에서 출발(x_0), 20m/s(v) 로 5s(t)간 이동하면 비행기의 위치는 다음과 같음
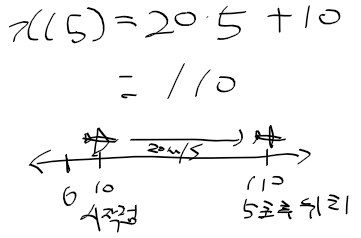
미분 방정식 분류
- 미분된 횟수(계)로 구분한다면 : 1계도함수, 2계 도함수...
1) 1계 1차 미방 : x가 한번 미분됨
2) 2계 1차 미방 : x가 2번 미분됨

- 선형/비선형으로 구분한다면 : 선형 미방, 비선형 미방
1) 선형 미방 : x가 1차임(x^2같은게 없으므로)
2) 비선형 미방 : x가 1차가 아님, 아래의 예시에서 sinx는 비선형 함수가 포함되있으므로 비선형 미방
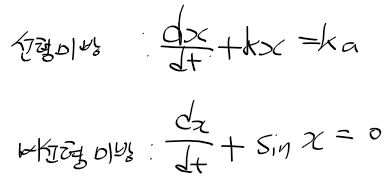
- 계수가 변수인지, 정해진 수인지에 따라 : 변계수 미방, 정계수 미방
1) 변계수 미방 : 계수가 변수로 된 경우, 아래 예시에서 m,v,k는 변수
2) 정계수 미방 : 계수가 정해진 수인경우, 아래 예시에서는 1, 2, 3으로 정해짐
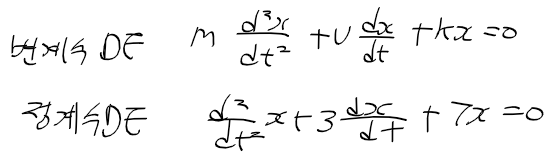
- 변수와 관계없는 계수(상수항)이 0인지 여부에 따라 : 비동차 미방, 동차 미방
1) 비동차 미방 : 우측의 상수항이 0이 아님
2) 동차 미방 : 우측의 상수항(x가 없는)이 0임
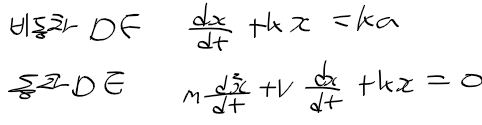
미분 방정식을 통한 현실의 물리 운동 표현의 예시
| 계수 | 종류 | 식 | 무엇을 표현할까 | |
| 1계 | 동차 선형 |  |
시간(t)에 따른 인구수(P) 변화를 표현하는 미방 | |
| 비동차 선형 | 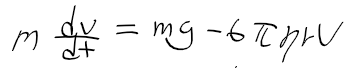 |
구름이 떨어지는 속도(v)를 나타내는 미방 (우항 mg - 6pi....는 중력과 점성 저항 표현) |
||
| 2계 | 동차 선형 | 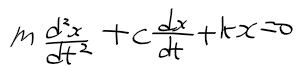 |
탄성과 저항(댐퍼?)를 고려한 진동 시스템 미방 | |
| 비동차 선형 | 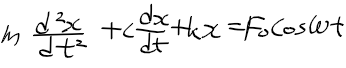 |
위 진동 시스템에 외력(F_0 cos 블라블라)이 가해지는 경우 미방 |
| 미분방정식으로 현실을 어떻게 수학 모델로 만들까 2 -비동차미방풀기 (0) | 2023.09.20 |
|---|---|
| 컴퓨터 과학 관련 용어 1. 인코딩, 데이터 규격, 프로세서 관련 (0) | 2022.05.30 |
| 네트워크 간단 요약 (0) | 2022.05.29 |
| 로봇 공학 요약 - 로봇 종류부터 구성 요소, 구동기, 센서까지 (0) | 2022.05.05 |
최근에는 메스프레소 영상 잘 보다가 이젠 볼게 다떨어져서
오랜만에 계속 봐야지 생각하던 만화로 쉽게배우는 시리즈의 미분 방정식 책을 봄
이 책을 보기 전에도 여러 차례 미분 방정식이 무엇인지 찾아보고
공업 수학을 이해하려고 시도는 했으나 잘 와닿지는 않았었다.
미분 방정식을 왜 만드는 것인지 이걸 어떻게 사용하는 것인지
기존의 책들에서는 초심자의 관점 보다는 수학자의 관점이라 해야할까
공업 수학 책같은거만 보면
미분 방정식의 공식 해 어떻게 계산하는것인지 사실들을 나열할 뿐
각 방식들마다 현실감에 와닿는 실제 사용 예시까지 자세히 설명하지는 않아서
미분 방정식을 학습하기에는 매우 어려운 편이었다.
어쨋든 이 책을 보기 전에는 미분 방정식은
현실의 물리적인 현상 계산하기 위해 표현한 것이 미분 방정식이고
기존의 대수 방정식은 특정한 값이 되는 해를 구하였다면
미분방정식의 경우 함수가 해가 되는 것이라고 정도 이해하였다.
(미분 방정식는 함수인 해를 구하는 것이다 이 조차도 최근 어디 만화로 쉽게배우는 시리즈 보다가 이해했다.)
미분 방정식이 현실을 반영하는 수학 모델이란걸 이해하면서 매우 중요한 개념인건 알고있으나
도통 현실에 어떻게 적용되는 것인지 이해하지 못한 상태에서 이 책을 보게 되었는데
역시 만화로 쉽게 배우는 시리즈가 정말 잘 만들어졌구나 감탄할수 밖에 없었다.
물론 기존의 공업 수학 교재 내용처럼 간결하거나 깊이 있지는 않지만
최대한 단순한 예제(뉴턴의 운동량 법칙)부터 시작해 단순한 미방 식의 해를 구하고
기존의 미방이 현실을 반영하지 못하면 현실을 더 반영해 실제와 유사해지는 미방을 만들어내는 과정이
그 망할 미분 방정식을 이렇게 설명해줄수 있구나 계속 놀라면서 보았다.
몇년전에 제어 공학에서 스프링 댐퍼 시스템을 공부하면서
기존의 교재로는 왜 이런 시스템이 있고 이것을 풀어가는지에 대한 이해를 거의 하지 못한채
억지로 공식만 외워 풀다가 잊어버리기를 반복했었는데
이 책을 보면서 질량 스프링 댐퍼 시스템도 전보다는 꽤 많이 이해할수 있었다.
아무튼 올해 전자정복과 더불어
몇 년동안 나를 속뒤집어지게 만들었던 미방을 어느정도 이해하게 도와준 가장 감명깊게 본 책
https://www.yes24.com/Product/Goods/5735225
만화로 쉽게 배우는 미분방정식 - 예스24
미분방정식의 세계를 유람하며 그림으로 재미있게 풀어낸 해설서! 미분방정식을 푸는 것은 어려운 일이다. 해답은 간단하게 발견되지 않는다. 하지만 이것은 일반론적인 이야기일 뿐이며, 해석
www.yes24.com
| 프로그래머를 위한 기초 해석학 (0) | 2023.09.21 |
|---|---|
| 만화로 쉽게 배우는 푸리에 해석 (0) | 2023.09.21 |
| 사영기하학, 위상수학 (0) | 2023.09.19 |
| 테일러급수, 유클리드 vs 비유클리드, 수학의 정의, 갈루아 등 (0) | 2023.09.18 |
| 수학을 잘한다의 진짜 의미 & 시험직후, 오답 정리를 안하는 이유 (0) | 2023.09.17 |
초등함수
- 다항함수, 지수함수, 로그함수 및 함수의 합성과 사칙연산으로 구할 수 있는 모든 함수
- (주의) 초월함수 : 대수적으로 구할수 없는 함수. 초월함수와 초등함수는 항상 같지 않음
* 지수함수, 로그함수, 삼각함수는 초등함수이면서 초월함수이기도 함(?)
=> 테일러 급수로 구할수 있어서 이들이 초등함수와 초월함수 둘다 포함되는건지 잘 모르겠음
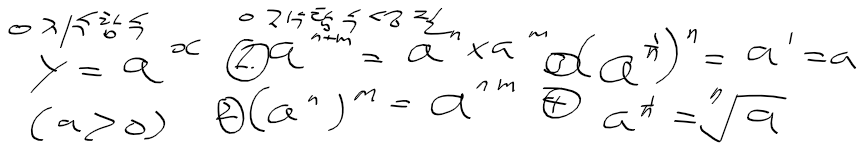
지수 함수
- 양의 상수 a( a > 0)이 주어질때 y = a^x인 함수
* 여기서 a가 왜 양수인 경우만 다루는지는 잘 모르겠음
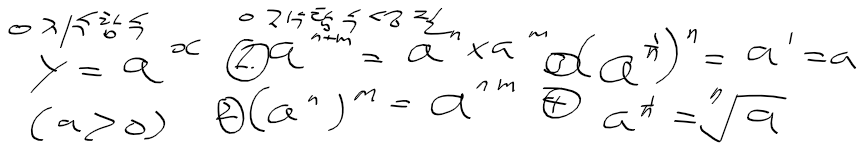
단조 증가와 단조 감소
- 지수함수는 a > 1인지 1 > a > 0 인지 여부에 따라 단조 증가, 단조 감소의 형태를 보임
- 추가로 지수 함수는 실수 전체에 정의되어 단조증가, 단조증가하나 치역(y 범위)는 양의 실수 공간임
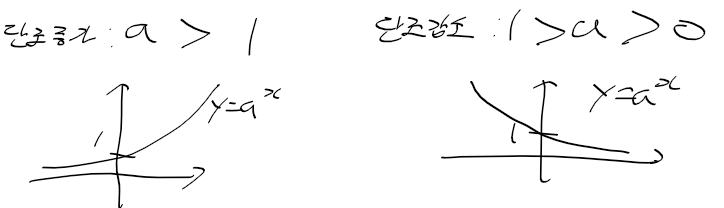
로그 함수
- 지수 함수를 역으로 하면 x = a^y를 만족하는 역함수가 존재함
- 로그 함수 : a를 밑(기저)로 하는 지수함수의 역함수
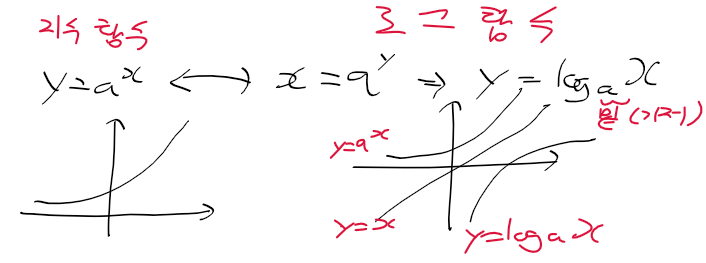
로그함수의 성질
- 로그 함수는 복잡한 곱샘 나눗셈을 단순한 덧셈, 뺄셈으로 변환해준다!
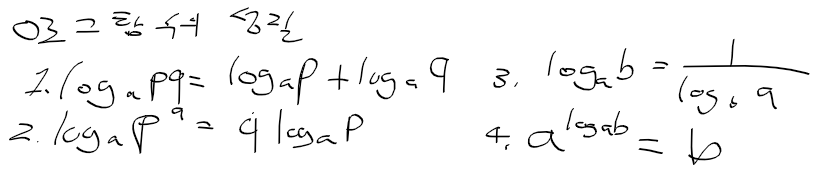
네이피어의 수
- 1에 가까워지는 1 + 1/x를 무한에 가까워지도록 x번 곱하면 (1 + 1/x)^x 했을때 수렴하는 수
- e = 2.712...
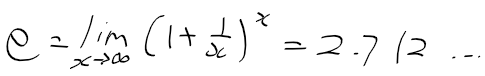
지수함수의 미분
- 도함수의 정의에 지수함수 f(x) = a^x를 대입하면 다음과 같이 지수함수의 도함수를 구할 수 있음
* 갑자기 f'(0)가 나오는 이유는 지수함수의 도함수식 x에다가 0을 대입하면 그대로 나오기 때문
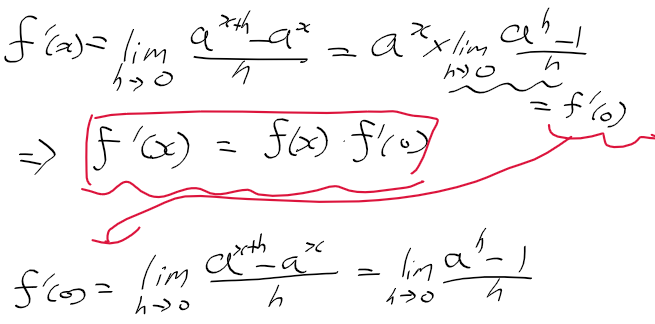
밑이 e인 지수함수의 미분이 자기자신인 이유
- 먼저 f'(0)에서 시작하자
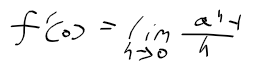
- 1) s = 1/(a^h - 1)를 정리하면 a^h = 1 + 1/s이 나온다. 이를 h에 대한 식으로 정리하자
- 2) s와 h에 대한 식을 f'(0)에 대입한다
- 3) f'(0) = 1/log_a_e가 나온다
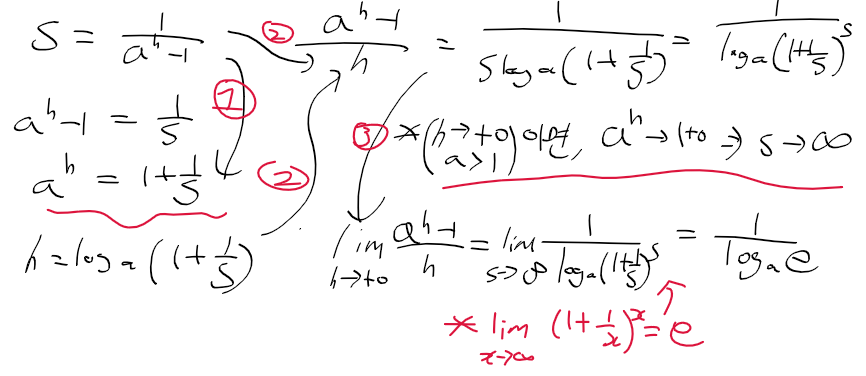
- 그러므로 지수함수 f(x)의 f'(0)는 log_e_a가 된다.
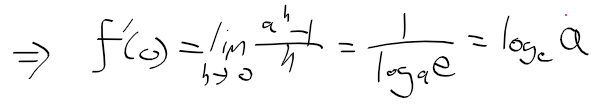
- 지수함수의 도함수 정리 결과에 a=e와 f'(0) = log_e_a를 대입하면 (e^x)' = e^x가 나온다
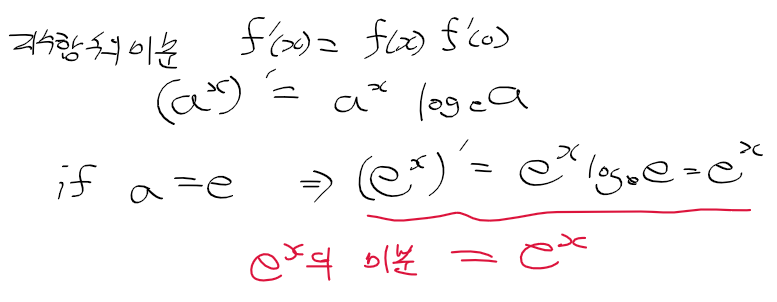
밑이 e인 지수함수와 역함수(자연로그)
- 지수함수의 역함수가 로그함수 이듯, 밑이 e인 지수함수의 경우에도 역함수는 로그
- 밑이 e인 로그함수를 자연로그라 부르며 ln x로 표기
- 밑이 e인 지수함수는 exp(x)로 표기
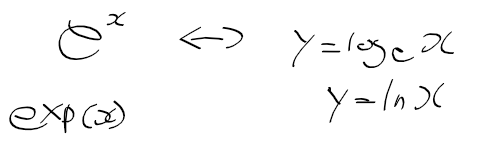
삼각함수와 도함수
- 반지름 길이가 1인 단위원과 0<= theta <= 2pi에서 x, y의 좌표
- 피타고라스 정리와 삼각함수 : cos^2 theta + sin^2 theta = 1
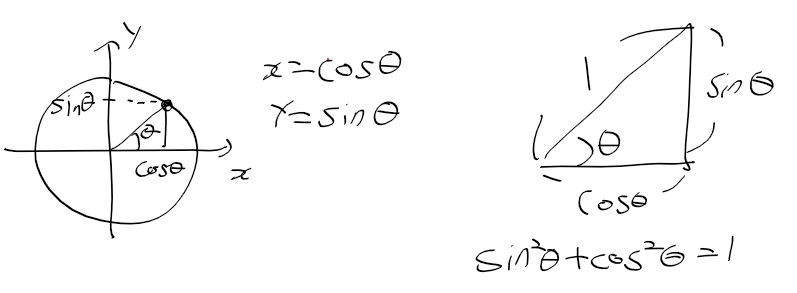
- 탄젠트 = 사인 / 코사인

- 삼각함수의 도함수 정리 하기 귀찬으므로 결과만 놓으면...
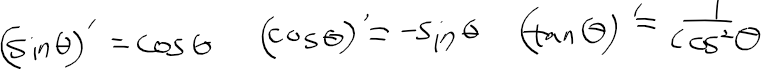
| 기초해석학 - 6. 테일러 근사와 해석 함수 (0) | 2023.09.21 |
|---|---|
| 기초해석학 - 5.무한소와 테일러 공식 (0) | 2023.09.21 |
| 기초해석학 - 3. 미적분 (0) | 2023.09.19 |
| 기초해석학 - 2. 함수 (0) | 2023.09.18 |
| 기초해석학 - 1. 집합과 사상 (0) | 2023.09.18 |